Đăng nhập Đăng ký

Câu hỏi:

2 năm trước

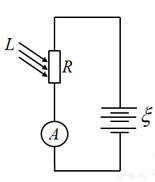
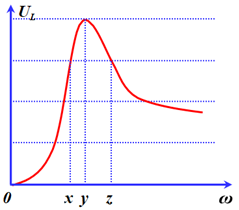
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P₁, P₂ và P₃. Biểu thức nào sau đây đúng?

$\dfrac{{{P_1} + {P_3}}}{8} = \dfrac{{{P_2}}}{9}$ .

$\dfrac{{{P_1} + {P_3}}}{9} = \dfrac{{{P_2}}}{8}$ .

$\dfrac{{{P_1} + {P_2}}}{{16}} = \dfrac{{{P_3}}}{9}$ .

$\dfrac{{{P_1} + {P_2}}}{9} = \dfrac{{{P_3}}}{{16}}$ .

Xem đáp án

133 lượt xem

Đề thi khoa học tự nhiên - Đề số 2 - Tự chọn - Đánh Giá Năng Lực. Thi ngay

Trả lời bởi giáo viên

Đáp án đúng: b

Điện áp hiệu dụng giữa hai đầu cuộn dây là:

${U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{U.{Z_L}}}{R}.\dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{U.{Z_L}.cos\varphi }}{R}$

Với tần số ω₁ = x; ω₂ = y và ω₃ = z, ta có:

$\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}} = \dfrac{2}{{{\omega _2}^2}}$

Từ đồ thị ta thấy:

$\begin{array}{l}{U_{L1}} = {U_{L3}} = \dfrac{3}{4}{U_{L2}} = \dfrac{3}{4}{U_{L\max }}\\ \Rightarrow \dfrac{{U.{Z_{L1}}\cos {\varphi _1}}}{R} = \dfrac{{U.{Z_{L3}}\cos {\varphi _3}}}{R} = \dfrac{3}{4}\dfrac{{U.{Z_{L2}}\cos {\varphi _2}}}{R}\\ \Rightarrow {\omega _1}^2{\cos ^2}{\varphi _1} = {\omega _3}^2{\cos ^2}{\varphi _3} = \dfrac{9}{{16}}{\omega _2}^2{\cos ^2}{\varphi _2}\\ \Rightarrow \left\{ \begin{array}{l}\dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}\dfrac{{{\omega ^2}}}{{{\omega _1}^2}}\\\dfrac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}\varphi }} = \dfrac{9}{{16}}\dfrac{{{\omega ^2}}}{{{\omega _2}^2}}\end{array} \right. \Rightarrow \dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \dfrac{{{{\cos }^2}{\varphi _3}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}{\omega ^2}.\left( {\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}}} \right)\\ \Rightarrow \dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \dfrac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}{\omega _2}^2.\dfrac{2}{{{\omega _2}^2}} = \dfrac{9}{8}\,\,\left( 1 \right)\end{array}$

Công suất tiêu thụ của mạch điện là:

$P = \dfrac{{{U^2}{{\cos }^2}\varphi }}{R} \Rightarrow P \sim {\cos ^2}\varphi$

Từ (1) ta có: $\dfrac{{{P_1}}}{{{P_2}}} + \dfrac{{{P_3}}}{{{P_2}}} = \dfrac{9}{8} \Rightarrow \dfrac{{{P_1} + {P_3}}}{9} = \dfrac{{{P_2}}}{8}$

Hướng dẫn giải:

Sử dụng kĩ năng đọc đồ thị

Điện áp U_Lmax khi tần số có giá trị ω₂

Hai tần số ω₁, ω₃ cho cùng giá trị điện áp ${U_L}:\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}} = \dfrac{2}{{{\omega _2}^2}}$

Độ lệch pha giữa điện áp và cường độ dòng điện: $\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}$

Điện áp hiệu dụng giữa hai đầu cuộn dây: ${U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}$

Công suất tiêu thụ: $P = \dfrac{{{U^2}{{\cos }^2}\varphi }}{R}$

Câu hỏi khác

Câu 1:

Một cây cầu bắc ngang qua sông Phô-tan-ka ở thành phố Xanh Pê-téc-bua (Nga) được thiết kế xây dựng đủ vững chắc, có thể cho cùng lúc 300 người đi qua mà cầu không sập. Năm 1906 có một trung đội bộ binh gồm 36 người đi đều bước qua cây cầu làm cho cây cầu gãy. Sự cố gãy cầu là do

dao động tuần hoàn của cầu.

xảy ra cộng hưởng cơ ở cầu.

cầu không chịu được tải trọng.

dao động tắt dần của cây cầu.

Xem đáp án

132

132 lượt xem
Xem đáp án
2 năm trước

Câu 2:

Một máy bơm sử dụng cho đài phun nước được nối bởi dây dẫn cách nguồn điện 18 m. Nguồn điện có hiệu điện thế hiệu dụng 230 V. Máy bơm hoạt động bình thường với điện áp hiệu dụng thấp nhất là 218 V và cường độ dòng điện 0,83 A. Điện trở lớn nhất trên mỗi mét chiều dài dây dẫn là bao nhiêu để máy bơm hoạt động bình thường?

$0,4\,\,\Omega /m$ .

$0,8\,\,\Omega /m$ .

$1,3\,\,\Omega /m$ .

$1,4\,\,\Omega /m$ .

Xem đáp án

135

135 lượt xem
Xem đáp án
2 năm trước

Câu 3:

Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng $216g$ và lò xo có độ cứng $k$ , dao động dưới tác dụng của ngoại lực $\text{F = }{{\text{F}}_{\text{0}}}\text{cos2 }\!\!\pi\!\!\text{ ft}$ , với ${{F}_{0}}$ không đổi và $f$ thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ $A$ của con lắc theo tần số $f$ có đồ thị như hình vẽ. Giá trị của $k$ gần nhất với giá trị nào sau đây?

Xem đáp án

137

137 lượt xem
Xem đáp án
2 năm trước

Câu 4:

Trên hình vẽ, ta có $\xi$ : bộ pin $9{\mkern 1mu} {\mkern 1mu} V - 1{\mkern 1mu} {\mkern 1mu} \Omega$ ; A: có thể là một ampe kế hoặc micrôampe kế; R là một quang điện trở; L à chùm sáng thích hợp chiếu vào quang điện trở. Khi không chiếu sáng vào quang điện trở thì số chỉ của micrôampe kế là $6{\mkern 1mu} {\mkern 1mu} \mu A$ . Khi quang điện trở được chiếu sáng thì ampe kế chỉ $0,6{\mkern 1mu} {\mkern 1mu} A$ . Tính điện trở của quang điện trở khi không được chiếu sáng và khi được chiếu sáng bằng ánh sáng thích hợp. Điện trở của ampe kế và của micrôampe kế coi như nhỏ không đáng kể.

${R_1} = 2{\mkern 1mu} {\mkern 1mu} M\Omega ;{\mkern 1mu} {\mkern 1mu} {R_2} = 19{\mkern 1mu} {\mkern 1mu} \Omega$

${R_1} = 1,5{\mkern 1mu} {\mkern 1mu} M\Omega ;{\mkern 1mu} {\mkern 1mu} {R_2} = 19{\mkern 1mu} {\mkern 1mu} \Omega$

${R_1} = 1,5{\mkern 1mu} {\mkern 1mu} M\Omega ;{\mkern 1mu} {\mkern 1mu} {R_2} = 14{\mkern 1mu} {\mkern 1mu} \Omega$

${R_1} = 2{\mkern 1mu} {\mkern 1mu} M\Omega ;{\mkern 1mu} {\mkern 1mu} {R_2} = 14{\mkern 1mu} {\mkern 1mu} \Omega$

Xem đáp án

116

116 lượt xem
Xem đáp án
2 năm trước

Câu 5:

Sóng dừng truyền trên sợi dây PQ. Biết P, R, Q là nút sóng. S và T là hai điểm trên dây cách R một khoảng x như hình vẽ. Phát biểu nào sau đây đúng về dao động của hai điểm S và T?

cùng biên độ và cùng pha.

khác biên độ và cùng pha.

cùng biên độ và lệch pha 180⁰.

khác biên độ và lệch pha 180⁰.

Xem đáp án

127

127 lượt xem
Xem đáp án
2 năm trước

Câu 6:

Trong thí nghiệm khe Young ta thu được hệ thống vân sáng, vân tối trên màn. Xét hai điểm $A,\,\,B$ đối xứng qua vân trung tâm, khi màn cách hai khe một khoảng là $D$ thì $A,\,\,B$ là vân sáng. Dịch chuyển màn ra xa hai khe một khoảng $d$ thì $A,\,\,B$ là vân sáng và đếm được số vân sáng trên đoạn $AB$ trước và sau khi dịch chuyển màn hơn kém nhau $4$ . Nếu dịch tiếp màn ra xa hai khe một khoảng $9d$ nữa thì $A,\,\,B$ lại là vân sáng và nếu dịch tiếp màn ra xa nữa thì tại $A$ và $B$ không còn xuất hiện vân sáng nữa. Tại $A$ khi chưa dịch chuyển màn là vân sáng thứ mấy?

Xem đáp án

123

123 lượt xem
Xem đáp án
2 năm trước