Một họa tiết như hình vẽ sau:
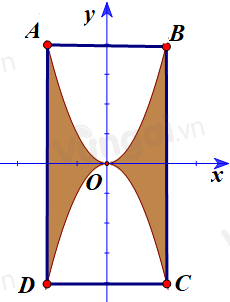
Phần tô đập được đính đá với giá thành 500 000 đ/\({m^2}\). Phần còn lại không được tô màu với giá thành 250 000 đ/\({m^2}\). Để trang trí 1000 họa tiết như vậy cần số tiền là bao nhiêu đồng (Làm tròn đến hàng đơn vị)
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Ta có: \(AB = 4dm,BC = 8dm\). Ta có các điểm: \(A\left( { - 2;4} \right),B\left( {2;4} \right),C\left( {2; - 4} \right),D\left( { - 2; - 4} \right)\)
Parabol trên Ox đi qua điểm O, A, B thì có phương trình dạng \(y = a.{x^2}\)
Khi đó: \(4 = a{.2^2} \Rightarrow a = 1 \Rightarrow y = {x^2}\)
Parabol trên Ox đi qua điểm O, C, D thì có phương trình dạng \(y = - {x^2}\)
Diện tích phần tô đậm là: \({S_1} = 4\int\limits_0^2 {{x^2}dx} = \dfrac{{32}}{3}\left( {d{m^2}} \right) = \dfrac{{32}}{3}{.10^{ - 2}}\left( {{m^2}} \right)\)
Diện tích hình chữ nhật là: S=4.8=32 \(\left( {d{m^2}} \right)\)
Diện tích phần không tô màu là: \({S_2} = S - {S_1} = \dfrac{{64}}{3}\left( {d{m^2}} \right) = \dfrac{{64}}{3}{.10^{ - 2}}\left( {{m^2}} \right)\)
Tổng chi phí trang trí là:
\(T = 1000.\left( {\dfrac{{32}}{3}{{.10}^{ - 2}}.500000 + \dfrac{{64}}{3}{{.10}^{ - 2}}.250000} \right)\)\( = 106666667\)đồng.
Hướng dẫn giải:
- Xác định tọa độ A,B, C, D và parabol
- Tính diện tích phần tô đậm và phần không tô đậm.
- Tính tổng chi phí trang trí 1000 họa tiết