Một electron đang chuyển động với vận tốc bắt đầu \({v_0} = 3,{2.10^6}m/s\) thì bay vào điện trường đều theo hướng cùng chiều đường sức điện trường. Biết cường độ điện trường có cường độ \(E = 910V/m\). Biết điện tích và khối lượng của electron lần lượt là \(e = - 1,{6.10^{ - 19}}C,\) \(m = 9,{1.10^{ - 31}}kg\). Thời gian t mà electron đi được cho đến khi dừng lại có giá trị nào sau đây? Cho rằng điện trường đủ rộng
Trả lời bởi giáo viên
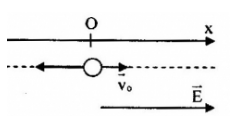
Chọn trục Ox có gốc O là vị trí mà electron bắt đầu bay vào điện trường, chiều dương trùng với chiều chuyển động.
+ Khi bay trong điện trường, electron chịu tác dụng của lực điện \(\overrightarrow F \)
+ Định luật II Niuton: \(\overrightarrow F = m\overrightarrow a \) (1)
Chiếu (1) lên Ox ta được: \( - F = ma\) (do \(e < 0 \Rightarrow \overrightarrow F \uparrow \downarrow \overrightarrow E \) )
\(\begin{array}{l} \Leftrightarrow - \left| e \right|E = ma\\ \Rightarrow a = \dfrac{{ - \left| e \right|E}}{m} = \dfrac{{ - \left| { - 1,{{6.10}^{ - 19}}} \right|.910}}{{9,{{1.10}^{ - 31}}}} = - 1,{6.10^{14}}\left( {m/{s^2}} \right)\end{array}\)
Phương trình vận tốc của electron: \(v = {v_0} + at = 3,{2.10^6} - 1,{6.10^{14}}t\)
Electron dừng lại khi \(v = 0\)
\(\begin{array}{l} \Leftrightarrow 0 = 3,{2.10^6} - 1,{6.10^{14}}t\\ \Rightarrow t = {2.10^{ - 8}}s\end{array}\)
Hướng dẫn giải:
+ Sử dụng biểu thức định luật II – Niuton: \(\overrightarrow F = m\overrightarrow a \)
+ Sử dụng biểu thức tính lực điện: \(F = qE\)
+ Sử dụng phương trình vận tốc của vật chuyển động biến đổi đều: \(v = {v_0} + at\)



