Một electron bay trong điện trường giữa hai bản kim loại đặt song song, đã tích điện và cách nhau \(2\,\,cm\), với vận tốc \({3.10^7}\,\,m/s\) theo phương song song với các bản. Khi electron đi được đoạn đường \(5\,\,cm\), nó bị lệch đi \(2,5\,\,mm\) theo phương của đường sức điện trong điện trường? Coi điện trường giữa hai bản là điện trường đều. Bỏ qua tác dụng của trọng lực của electron. Hiệu điện thế giữa hai bản gần giá trị nào sau đây nhất?
Trả lời bởi giáo viên
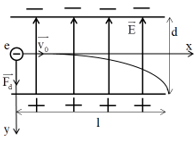
Gia tốc của electron là: \(a = \dfrac{{{F_d}}}{m} = \dfrac{{e.E}}{m} = \dfrac{{e.U}}{{m.d}}\)
Gia tốc theo phương Ox là: \({a_x} = 0\)
Gia tốc theo phương Oy là: \({a_y} = \dfrac{{eU}}{{md}}\)
Vận tốc theo phương Ox và Oy là:
\(\left\{ \begin{array}{l}{v_x} = {v_0}\\{v_y} = {v_{0y}} + {a_y}.t = \dfrac{{eU}}{{md}}.t\end{array} \right.\)
Phương trình chuyển động của electron theo phương Ox và Oy là:
\(\left\{ \begin{array}{l}x = {x_0} + {v_{0x}}t + \dfrac{1}{2}{a_x}.{t^2} = {v_0}.t \Rightarrow t = \dfrac{x}{{{v_0}}}\\y = {y_0} + {v_{0y}}.t + \dfrac{1}{2}{a_y}{t^2} = \dfrac{1}{2}.\dfrac{{eU}}{{md}}{t^2} = \dfrac{{eU}}{{2md.{v_0}^2}}.{x^2}\end{array} \right.\)
Thay số ta có:
\(2,{5.10^{ - 3}} = \dfrac{{1,{{6.10}^{ - 19}}.U}}{{2.9,{{1.10}^{ - 31}}.0,02.{{\left( {{{3.10}^7}} \right)}^2}}}.0,{05^2} \Rightarrow U = 204,75\,\,\left( V \right)\)
Hướng dẫn giải:
Sử dụng lý thuyết chuyển động ném ngang