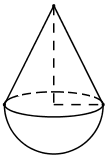
Một đồ chơi bằng gỗ có dạng một khối nón và một nửa khối cầu ghép với nhau (hình bên). Đường sinh của khối nón bằng 5 cm, đường cao của khối nón là 4 cm. Thể tích của đồ chơi bằng:

Tính tổng tất cả các nghiệm của phương trình \((2\cos 2x + 5)\left( {{{\sin }^4}x - {{\cos }^4}x} \right) + 3 = 0\) trên khoảng \((0;2\pi )\).

Mặt sàn tầng trệt ngôi nhà cao hơn mặt sân \(0,4\;{\rm{m}}\). Cầu thang đi tầng trệt lên tầng hai có 51 bậc, mỗi bậc cao \(22\;{\rm{cm}}\). Độ cao của tầng hai so với mặt sân là:

Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là 0,6 . Người đó bắn hai viên đạn một cách độc lập. Xác suất để một viên đạn bắn trúng mục tiêu và một viên đạn bắn trượt mục tiêu là:

Trong một nông trường chăn nuôi bò sữa ta thu nhập được số liệu sau:

Số con bò cho sản lượng sữa hàng ngày thấp nhất của nông trường là bao nhiêu ?

Một cái cổng hình parabol có dạng \(y =  - \frac{1}{2}{x^2}\) có chiều rộng \(d = 4m.\)

Tính chiều cao \(h\) của cổng (xem hình minh họa)

Với những giá trị nào của \(m\) thì đường thẳng \(\left( \Delta  \right):\,\,3x + 4y + 3 = 0\) tiếp xúc với đường tròn \(\left( C \right):\,\,{(x - m)^2} + {y^2} = 9\)?