Câu hỏi:
2 năm trước
Một đĩa tròn mỏng bằng gỗ, bán kính R = 5cm nổi trên mặt nước. Ở tâm đĩa có gắn một cây kim, thẳng đứng, chìm trong nước có chiết suất n = 4/3. Dù đặt mắt ở đâu cũng không thấy cây kim. Chiều dài tối đa của cây kim là:
Trả lời bởi giáo viên
Đáp án đúng: a
Hướng dẫn giải:
Ta có:
+ Góc giới hạn phản xạ toàn phần: \(\sin {i_{gh}} = \frac{{{n_{kk}}}}{{{n_{nuoc}}}} = \frac{1}{{\frac{4}{3}}} = \frac{3}{4}\)
Gọi O - tâm đĩa tròn, càng xa O thì góc tới i càng tăng, để không có tia sáng nào lọt ra ngoài không khí thì ngay tại vị trí xa O nhất, tại đó vừa bắt đầu xảy ra hiện tượng phản xạ toàn phần.
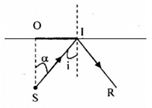
Ta có:
\(\begin{array}{l}\alpha = i = {i_{gh}}\\\sin \alpha = \frac{{OI}}{{SI}} = \frac{{OI}}{{\sqrt {O{I^2} + O{S^2}} }} = \sin {i_{gh}} = \frac{3}{4}\\ \to O{S^2} = \frac{7}{9}{\rm{O}}{{\rm{I}}^2} \to {\rm{OS = }}\sqrt {\frac{7}{9}} OI = \sqrt {\frac{7}{9}} .5 = 4,41cm\end{array}\)
Hướng dẫn giải:
+ Sử dụng hệ thức lượng giác trong tam giác
+ Vận dụng biểu thức tính góc giới hạn: \(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 6: khúc xạ ánh sáng - đề số 2 Lý 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: khúc xạ ánh sáng - đề số 3 Lý 11 có lời giải chi tiết
- Kiểm tra 1 tiết chương 6: Khúc xạ ánh sáng - Đề số 1 môn Lý lớp 11 có lời giải chi tiết
- Kiểm tra 15 phút chương 6: Khúc xạ ánh sáng - Đề số 1 môn Lý lớp 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 6: khúc xạ ánh sáng - đề số 3 Lý 11 có lời giải chi tiết
