Câu hỏi:
2 năm trước
Một con lắc lò xo đang dao động điều hòa, lực đàn hồi của lò xo phụ thuộc vào chiều dài của lò xo như đồ thị hình vẽ. Cho \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Biên độ và chu kì dao động của con lắc là
Trả lời bởi giáo viên
Đáp án đúng: b
+ Từ đồ thị ta có:
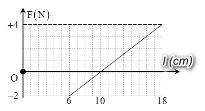
- Chiều dài cực đại của con lắc lò xo: \({l_{{\rm{max}}}} = 18cm\)
- Chiều dài nhỏ nhất của con lắc lò xo: \({l_{\min }} = 6cm\)
+ Biên độ dao động của vật:\(A = \dfrac{{{l_{max}} - {l_{\min }}}}{2} = \dfrac{{18 - 6}}{2} = 6cm\)
Chiều dài của con lắc khi ở vị trí cân bằng: \({l_{cb}} = {l_{{\rm{max}}}} - A = 18 - A = 18 - 6 = 12cm\)
+ Ta để ý rằng, tại vị trí lò xo không biến dạng (lực đàn hồi bằng 0) lò xo có chiều dài là \(10{\rm{ }}cm\)
=> Độ dãn của lò xo tại vị trí cân bằng:
\( \Rightarrow \Delta {l_0} = 12 - 10 = 2cm \Rightarrow T = 2\pi \sqrt {\dfrac{{\Delta {l_0}}}{g}} = 0,28s\)
Hướng dẫn giải:
+ Đọc đồ thị $F – l$
+ Sử dụng biểu thức: \(A = \dfrac{{{l_{{\rm{max}}}} - {l_{\min }}}}{2}\)
+ Vận dụng biểu thức tính độ dãn của lò xo tại vị trí cân bằng: \(\Delta {l_0} = \dfrac{{mg}}{k}\)
+ Sử dụng biểu thức tính chu kì: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 2\pi \sqrt {\dfrac{{\Delta {l_0}}}{g}} \)
Câu hỏi khác
- Đề thi thử thpt qg sở gdđt hà nội - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt chuyên lam sơn - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 01 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg sở gdđt kiên giang - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 02 Lý 12 có lời giải chi tiết
