Câu hỏi:
2 năm trước
Một cái máng nước sâu 30 cm rộng 40 cm có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến một độ cao h thì bóng của thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của nước là n = \(\frac{4}{3}\). h = ?
Trả lời bởi giáo viên
Đáp án đúng: c
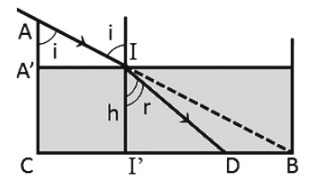
Ta có: \(\tan i = \frac{{CI'}}{{AA'}} = \frac{{CB}}{{AC}} = \frac{{40}}{{30}} = \frac{4}{3} \to i = {53,1^0}\)
Theo định luật khúc xạ ánh sáng, ta có:
\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \to {\rm{sinr}} = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{1.sin{{53,1}^0}}}{{\frac{4}{3}}} = 0,6 \to r = {36,87^0}\)
Mặt khác, từ hình ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\tan i = \frac{{I'B}}{h}\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{I'B - DB}}{h}\end{array} \right. \to \frac{{\tan i}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \frac{{I'B}}{{I'B - DB}} = \frac{{16}}{9} \to I'B = \frac{{16}}{7}DB = \frac{{16}}{7}.7 = 16cm\\ \to h = \frac{{I'B}}{{\tan i}} = 12cm\end{array}\)
h = 12 (cm).
Hướng dẫn giải:
+ Sử dụng các hệ thức lượng trong tam giác
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
