Câu hỏi:
2 năm trước
Một bể nước cao h = 80cm chứa đầy nước, một người đặt mắt nhìn xuống đáy bể theo phương gần vuông góc thấy đáy bể cách mắt mình 110cm. Hỏi người này đặt mắt cách mặt nước bao nhiêu? Biết chiết suất của nước là 4/3
Trả lời bởi giáo viên
Đáp án đúng: c
Gọi A là đáy bể thật và A’ là ảnh của đáy chậu
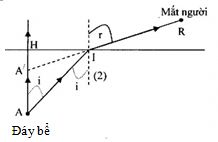
Từ hình vẽ, ta có:
\(\left\{ \begin{array}{l}\tan i = \frac{{HI}}{{HA}}\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \frac{{HI}}{{HA'}}\end{array} \right.\)
Vì mắt người nhìn xuống đáy chậu gần vuông góc nên góc i, r nhỏ
i, r nhỏ nên ta có:\(\tan i \approx \sin i \approx i;{\rm{ tanr}} \approx {\rm{sinr}} \approx r\)
+ Theo định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}n\sin i = 1.{\mathop{\rm s}\nolimits} {\rm{inr}} \to \frac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = \frac{1}{n} = \frac{{HA'}}{{HA}}\\ \to HA' = \frac{{HA}}{n} = \frac{{80}}{{\frac{4}{3}}} = 60cm\end{array}\)
Khoảng cách từ mặt nước tới ảnh của đáy chậu là
+ Khi người này nhìn vào chậu và thấy chậu cách mắt mình 110cm, khoảng cách này chính là khoảng cách từ mắt người quan sát đến ảnh A’ của đáy chậu
=> Khoảng cách từ mắt người đến mặt nước là: d = 110 - 60 = 50cm
Hướng dẫn giải:
+ Vẽ đường truyền của tia sáng qua lưỡng chất phẳng
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
+ Sử dụng hệ thức lượng giác
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 6: khúc xạ ánh sáng - đề số 2 Lý 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: khúc xạ ánh sáng - đề số 3 Lý 11 có lời giải chi tiết
- Kiểm tra 1 tiết chương 6: Khúc xạ ánh sáng - Đề số 1 môn Lý lớp 11 có lời giải chi tiết
- Kiểm tra 15 phút chương 6: Khúc xạ ánh sáng - Đề số 1 môn Lý lớp 11 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 6: khúc xạ ánh sáng - đề số 3 Lý 11 có lời giải chi tiết
