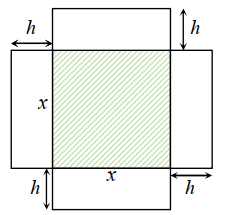
Một bác thợ gò hàn làm một chiếc thùng hình hộp chữ nhật (không nắp) bằng tôn thể tích 665,5\(d{m^3}\). Chiếc thùng này có đáy là hình vuông cạnh x (dm) , chiều cao h (dm) . Để làm chiếc thùng, bác thợ phải cắt một miếng tôn như hình vẽ. Tìm x để bác thợ sử dụng ít nguyên liệu nhất
Chỉ điền số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Ta có: \(V = {x^2}.h = 665,5 \Rightarrow h = \dfrac{{665,5}}{{{x^2}}}\left( {x > 0} \right)\)
Tổng diện tích của các mặt là:
\(\begin{array}{l}S = {x^2} + 4.x.h = {x^2} + \dfrac{{2662}}{x}\\ \Rightarrow S' = 2x - \dfrac{{2662}}{{{x^2}}}\\S' = 0 \Leftrightarrow x = 11\end{array}\)
Lập bảng biến thiên:
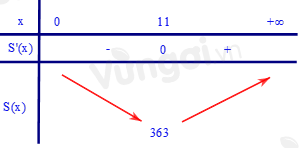
Ta thấy khi x=11 thì S đạt giá trị nhỏ nhất.
Vậy để sử dụng ít nguyên liệu nhất thì bác thợ gò phải cắt một miếng tôn có đáy là hình vuông cạnh 11 (dm).
Hướng dẫn giải:
- Biểu diễn h theo x
- Lập công thức tính diện tích các mặt S theo x
- Xét hàm số S=S(x) và tìm min.
- Tìm x.


