Câu hỏi:
2 năm trước
Một anten parabol, đặt tại một điểm A trên mặt đất, phát ra một sóng truyền theo phương làm với mặt phẳng ngang góc 450 hướng lên một vệ tinh địa tĩnh V. Coi trái đất là hình cầu, bán kính R=6380km. Vệ tinh địa tĩnh ở độ cao 35800km so với mặt đất. Sóng này truyền từ A đến V mất thời gian:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có:
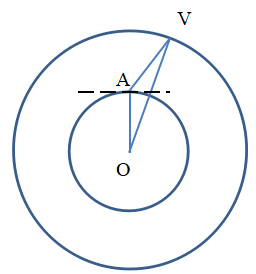
Ta có: OV = OA + h = 6380 + 35800 = 42180 (km)
Theo định lí hàm cos ta có:
\(O{V^2} = O{A^2} + A{V^2} - 2{\rm{O}}A.AV.\cos \left( {{{135}^0}} \right)\)
\( \Rightarrow {42180^2} = {6380^2} + A{V^2} - 2.\left( {\frac{{ - \sqrt 2 }}{2}} \right).6380.AV\)
\( \Rightarrow A{V^2} + \sqrt 2 .6380.AV + {6380^2} - {42180^2} = 0\)
\( \Rightarrow AV \approx 37500\left( {km} \right)\)
Mặt khác, ta có:
\(\begin{array}{l}AV = ct\\ \to t = \dfrac{{AV}}{c}=\dfrac{{37500.1000}}{{{{3.10}^8}}}=0,125{\rm{s}}\end{array}\)
Hướng dẫn giải:
+ Vẽ hình
+ Sử dụng hệ thức lượng trong tam giác
+ Vận dụng công thức : \(s = vt\)
