Câu hỏi:
2 năm trước
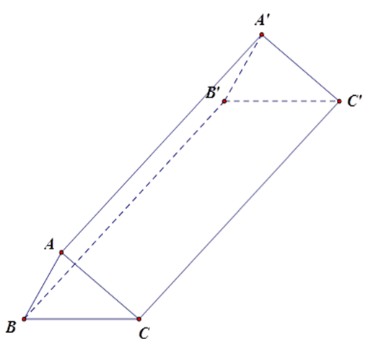
Hình lăng trụ đứng $ABC.A'B'C'$ (hình vẽ) có \(\widehat {BAC} = {90^0},AB = 6cm,AC = 8cm,{\rm{AA' = 15cm}}\) . Diện tích toàn phần của hình lăng trụ đó bằng
Trả lời bởi giáo viên
Đáp án đúng: d
Áp dụng định lý Pytago cho tam giác \(ABC\) ta được $B{C^2} = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10\,cm$ .
Ta có chu vi đáy \({P_{ABC}} = AB + AC + BC = 6 + 8 + 10 = 24\,cm\)
Diện tích đáy \({S_{ABC}} = \dfrac{{AB.AC}}{2} = \dfrac{{6.8}}{2} = 24\,c{m^2}\) .
Diện tích xung quanh của lăng trụ đứng \({S_{xq}} = 24.15 = 360\,c{m^2}\) .
Diện tích toàn phần ${S_{tp}} = 360 + 2.24 = 408\,c{m^2}$ .
Hướng dẫn giải:
Sử dụng cách tính diện tích toàn phần hình lăng trụ đứng.
Diện tích toàn phần của hình lăng trụ đứng bằng tổng của diện tích xung quanh và diện tích hai đáy
Câu hỏi khác
- Đề kiểm tra 15 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 8: hình lăng trụ đứng. hình chóp đều - đề số 2 Toán 8 có lời giải chi tiết
