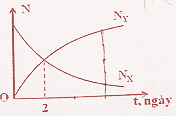
Hạt nhân X bị phóng xạ thành hạt nhân bền Y. Hình bên là đồ thị biểu diễn sụ phụ thộc của số hạt nhân X và số hạt nhân Y theo thời gian. Lúc \(t = 6\) ngày, tỷ số giữa hạt nhân X và số hạt nhân Y là:

Số hạt nhân X còn lại sau thời gian t là \({N_X} = {N_0}{.2^{ - \dfrac{t}{T}}}\)

Số hạt nhân Y sinh ra sau thời gian t là \({N_Y} = {N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\)

Từ đồ thị ta thấy tại \(t = 2\) ngày số hạt nhân X bằng số hạt nhân Y nên ta có

\({N_0}{2^{\dfrac{{-2}}{T}}} = {N_0}\left( {1 - {2^{ - \dfrac{2}{T}}}} \right) =  > {2^{-\dfrac{{2}}{T}}} = \dfrac{1}{2} =  >  - \dfrac{{2}}{T} =  - 1 \)

=> \(T = 2\) ngày

Vậy tại \(t = 6\) ngày, tỷ số giữa hạt nhân X và số hạt nhân Y là \(\dfrac{{{N_X}}}{{{N_Y}}} = \dfrac{{{N_0}{{.2}^{\dfrac{{ - 6}}{2}}}}}{{{N_0}\left( {1 - {2^{ - \dfrac{6}{2}}}} \right)}} = \dfrac{{\dfrac{1}{8}}}{{\dfrac{7}{8}}} = \dfrac{1}{7}\)