Hai thấu kính được ghép đồng trục, thấu kính \({L_1}\) có tiêu cự \({f_1} = {\rm{ }}10{\rm{ }}cm\), thấu kính \({L_2}\) có tiêu cự \({f_2} = - {\rm{ }}10{\rm{ }}cm\). Khoảng cách giữa hai kính là \(a{\rm{ }} = {\rm{ }}40{\rm{ }}cm\). Phía ngoài hệ, trước \({L_1}\) có vật sáng AB vuông góc với trục chính hệ thấu kính tại A, cách \({L_1}\) \(15cm\). Ảnh cuối cùng qua hệ là
Trả lời bởi giáo viên
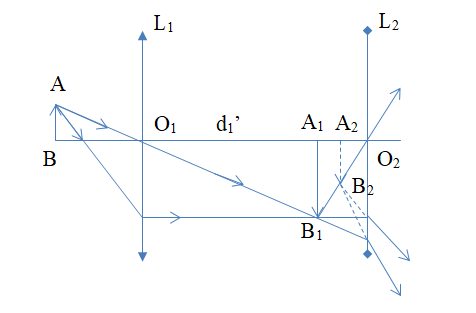
+ Qua \({L_1}\) vật \(AB\) có ảnh \({A_1}{B_1}\) cách \({L_1}\) là:
\({d_1}' = \dfrac{{{d_1}{f_1}}}{{{d_1} - {f_1}}} = \dfrac{{15.10}}{{15 - 10}} = 30cm\)
Số phóng đại \({k_1} = - \dfrac{{{d_1}'}}{{{d_1}}} = - \dfrac{{30}}{{15}} = - 2\).
+ Hình vẽ cho thấy, \({A_1}{B_1}\) cách thấu kính \({L_2}\) một đoạn:
\({d_2} = {\rm{ }}a{\rm{ }} - {d_1}'{\rm{ }} = {\rm{ }}40{\rm{ }} - {\rm{ }}30{\rm{ }} = {\rm{ }}10{\rm{ }}cm\)
+ Ánh sáng truyền qua \({L_1}\) hội tụ tại \({A_1}{B_1}\) rồi lại truyền tiếp tới \({L_2}\).
Do vậy \({A_1}{B_1}\) lại là vật sáng đối với \({L_2}\)
+ Vận dụng công thức thấu kính với \({L_2}\), ta được:
\({d_2}' = \dfrac{{{d_2}{f_2}}}{{{d_2} - {f_2}}} = \dfrac{{10.( - 10)}}{{10 + 10}} = - 5cm\)
\({k_2} = - \dfrac{{{d_2}'}}{{{d_2}}} = \dfrac{1}{2}\)
+ Số phóng đại ảnh của hệ thấu kính:
\(k = \dfrac{{\overline {{A_2}{B_2}} }}{{\overline {AB} }} = \dfrac{{\overline {{A_2}{B_2}} }}{{\overline {{A_1}{B_1}} }}.\dfrac{{\overline {{A_1}{B_1}} }}{{\overline {AB} }} = {k_2}.{k_1}\)
\(k = - 1\)
+ Vậy ảnh cuối cùng của hệ là ảnh ảo, cao bằng vật, ngược chiều với vật, cách \({L_2}\) một đoạn \(5cm\)
Hướng dẫn giải:
+ Vẽ ảnh của vật qua hai thấu kính
+ Sử dụng công thức thấu kính: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
+ Sử dụng biểu thức xác định hệ số phóng đại: \(k = - \dfrac{{d'}}{d} = \dfrac{{A'B'}}{{AB}}\)

