Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng hai sợi dây không dãn, dài 10 cm. Tích điện cho mỗi quả cầu điện tích q như nhau thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 60⁰. Tính độ lớn điện tích mà ta đã truyền cho hai quả cầu. Lấy g = 10 (m/s²).

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Biểu diễn các lực tác dụng lên quả cầu:

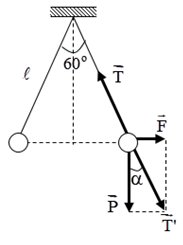
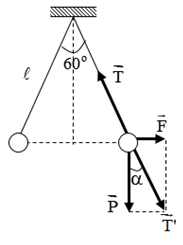
+ Từ hình vẽ ta có:

\(\begin{array}{l}\tan \alpha  = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha  = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 30 = 0,029N\end{array}\)

+ Khi hai dây treo hợp với nhau một góc 60⁰thì khoảng cách giữa hai điện tích bằng:

\(l = 10cm = 0,1m\)

+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{l^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{l^2}}}{k}} \)

Thay số ta được: \(\left| q \right| = \sqrt {\dfrac{{0,029.0,{1^2}}}{{{{9.10}^9}}}}  = 1,{8.10^{ - 7}}C\)

+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2.\left| q \right| = 3,{6.10^{ - 7}}\;C\)