Câu hỏi:
2 năm trước
Hai dây dẫn thẳng dài, đặt song song, cách nhau $10 cm$ trong không khí, có hai dòng điện ngược chiều, có cường độ $I_1= 6 A$; $I_2= 12 A$ chạy qua. Cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm $M$ cách dây dẫn mang dòng $I_1$ một đoạn $5 cm$ và cách dây dẫn mang dòng $I_2$ một đoạn $15 cm$ là bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: a
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi ra tại B thì các dòng điện I1 và I2 gây ra tại M các véc tơ cảm ứng từ \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) có phương chiều như hình vẽ:
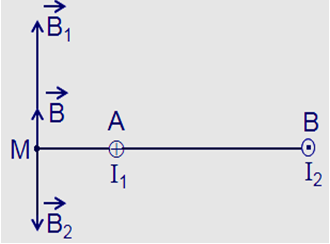
Có độ lớn: \({B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {\rm{ }}2,{4.10^{ - 5}}T;{\rm{ }}{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{BM}} = {\rm{ }}1,{6.10^{ - 5}}T.\)
Cảm ứng từ tổng hợp tại M là: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Vì \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) cùng phương, ngược chiều và B1 > B2 nên \(\mathop B\limits^ \to \) cùng phương, chiều với \(\mathop {{B_1}}\limits^ \to \) và có độ lớn: B = B1 - B2 = 0,8.10-5 T
Hướng dẫn giải:
- Áp dụng các bước giải xác định cảm ứng từ (Xem lí thuyết phần V)
- Áp dụng biểu thức xác định cảm ứng từ của dòng điện thẳng: \(B = {2.10^{ - 7}}\dfrac{I}{r}\).
