Câu hỏi:
2 năm trước
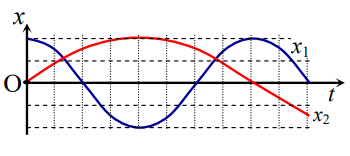
Hai chất điểm có cùng khối lượng, dao động điều hòa trên hai đường thẳng song song, có vị trí cân bằng cùng thuộc một đường thẳng vuông góc với các quỹ đạo. Đồ thị biểu diễn sự phụ thuộc của li độ x1 và x2 của hai chất điểm theo thời gian t như hình bên. Kể từ t = 0, thời điểm hai chất điểm có cùng li độ lần thứ 2021 thì tỉ số động năng của hai chất điểm \(\frac{{{{\rm{W}}_{d2}}}}{{{{\rm{W}}_{d1}}}}\) là
Trả lời bởi giáo viên
Đáp án đúng: b
Từ đồ thị ta thấy hai chất điểm có biên độ bằng nhau và bằng A
Chu kì dao động của chất điểm thứ 2: \({T_2} = 2{T_1} \Rightarrow {\omega _2} = \frac{{{\omega _1}}}{2}\)
Hai chất điểm có cùng li độ x1 = x2, ta có:
\(\frac{{{{\rm{W}}_{d2}}}}{{{{\rm{W}}_{d1}}}} = \frac{{\frac{1}{2}m{\omega _2}^2\left( {{A^2} - {x_2}^2} \right)}}{{\frac{1}{2}m{\omega _1}^2\left( {{A^2} - {x_1}^2} \right)}} = \frac{{{\omega _2}^2}}{{{\omega _1}^2}} = \frac{1}{4} = 0,25\)
Hướng dẫn giải:
Sử dụng kĩ năng đọc đồ thị
Động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right)\)
Câu hỏi khác
- Đề thi thử thpt qg sở gdđt hà nội - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt chuyên lam sơn - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg sở gdđt kiên giang - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 01 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt kim liên (2021) Lý 12 có lời giải chi tiết
