Giá trị nhỏ nhất của hàm số \(y = \left( {20{x^2} + 20x - 1283} \right){e^{40x}}\) trên tập hợp các số tự nhiên là:
Trả lời bởi giáo viên
Ta có \({y^\prime } = (40x + 20){e^{40x}} + 40\left( {20{x^2} + 20x - 1283} \right){e^{40x}} = 20{e^{40x}}\left( {40{x^2} + 42x - 2565} \right)\)
\({y^\prime } = 0 \Leftrightarrow 40{x^2} + 42x - 2565 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \dfrac{{15}}{2}}\\{x = - \dfrac{{171}}{{20}}}\end{array}} \right.\)
Đặt \({y_1} = y\left( { - \dfrac{{171}}{{20}}} \right);{y_2} = y\left( {\dfrac{{15}}{2}} \right)\)
\(y(7) = - 163.{e^{280}};y(8) = 157.{e^{320}}\)
Bảng biến thiên
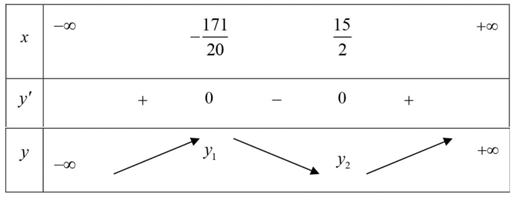
Dựa vào bảng biến thiên ta có giá trị nhỏ nhất của hàm số \(y = \left( {20{x^2} + 20x - 1283} \right){e^{40x}}\) trên tập hợp các số tự nhiên là \( - 163.{e^{280}}\).
Hướng dẫn giải:
- Giải phương trình \(y' = 0\) và lập bảng biên thiên.
- Dựa vào bảng biến thiên và kết luận.


