Câu hỏi:
2 năm trước
Đoạn mạch xoay chiều RLC nối tiếp , cuộn dây thuần cảm với \(C{R^2} < 2L\); điện áp hai đầu đoạn mạch là \(u = U\sqrt 2 cos\omega t\), U ổn định và \(\omega \) thay đổi . Khi \(\omega = {\omega _L}\) thì điện áp hai cuộn cảm L cực đại và \({U_{Lmax}} = \dfrac{{26U}}{{24}}\). Hệ số công suất tiêu thụ của cả đoạn mạch là :
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: \({U_{{L_{max}}}} = I.{Z_L} = \dfrac{U}{Z}.{Z_L}\)
Theo đầu bài, ta có: \({U_{Lmax}} = \dfrac{{26}}{{24}}U\)
Ta có thể giả sử: \(Z = 24\Omega ;{Z_L} = 26\Omega \)
Khi đó:
\(\begin{array}{l}Z_L^2 = {Z^2} + Z_C^2\\ \Rightarrow {Z_C} = \sqrt {Z_L^2 - {Z^2}} = \sqrt {{{26}^2} - {{24}^2}} = 10\Omega \end{array}\)
Lại có:
\(\begin{array}{l}\dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right)\\ \Rightarrow R = \sqrt {2{Z_C}\left( {{Z_L} - {Z_C}} \right)} = \sqrt {2.10\left( {26 - 10} \right)} = 8\sqrt 5 \Omega \end{array}\)
Hệ số công suất của mạch khi đó: \(cos\varphi = \dfrac{R}{Z} = \dfrac{{8\sqrt 5 }}{{24}} = \dfrac{{\sqrt 5 }}{3}\)
Hướng dẫn giải:
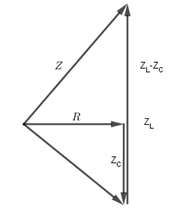
+ Sử dụng giản đồ véc-tơ
+ \(\omega \) thay đổi để \({U_{{L_{max}}}}\) khi đó: \(Z_L^2 = {Z^2} + Z_C^2\) và \(\dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right)\)
+ Sử dụng biểu thức tính hệ số công suất: \(cos\varphi = \dfrac{R}{Z}\)
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 3: dòng điện xoay chiều - đề số 03 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 3: dòng điện xoay chiều - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 03 Lý 12 có lời giải chi tiết
