Câu hỏi:
2 năm trước
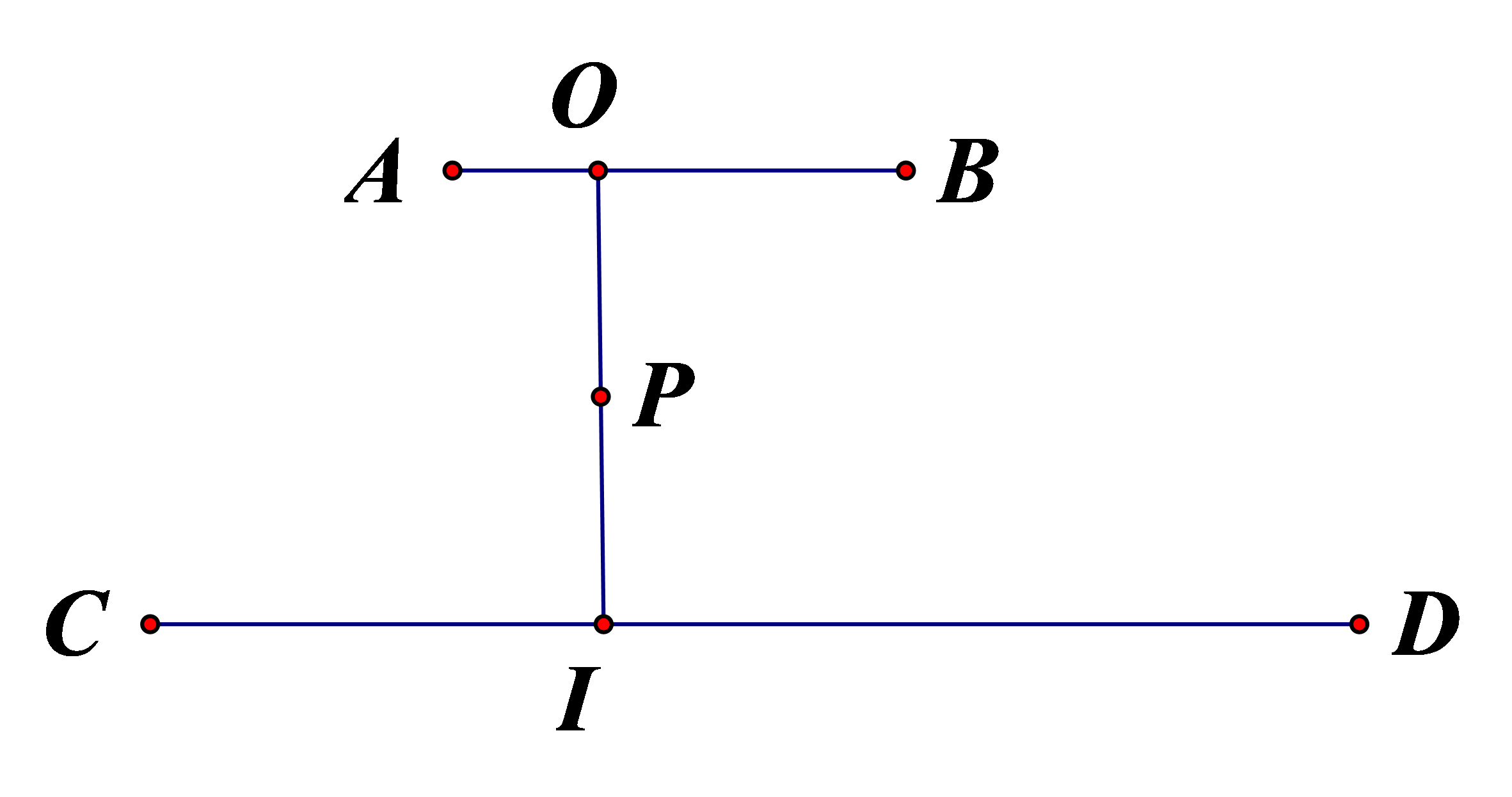
Đoạn đường AB dài \(2345\,m\) và đoạn đường CD dài \(4\,km\). Hai doạn đường này có chung nhau một cây cầu từ C đến B dài \(400\,m\)
Độ dài của đoạn đường từ A đến D là:
$m$
Trả lời bởi giáo viên
Đáp án:
Độ dài của đoạn đường từ A đến D là:
$m$
Đổi: \(4\,km = 4000\,m\)
Đoạn đường AC dài số mét là:
\(2345 - 400 = 1945\,\left( m \right)\)
Đoạn đường AD dài số mét là:
\(1945 + 4000 = 5945\,\left( m \right)\)
Đáp số: \(5945\,m\).
Số cần điền vào chỗ trống là \(5945\)
Hướng dẫn giải:
- Tìm độ dài đoạn thẳng AC.
- Tìm độ dài đoạn thẳng AD bằng tổng của hai đoạn thẳng AC và CD.
Giải thích thêm:
- Ngoài cách giải này, em có thể thấy, trong đoạn thẳng AB và CD đều có chứa đoạn thẳng BC nên nếu em tính AB+CD=AD+BC
Mà em đã biết độ dài của AB, CD, BC. Từ đó em có thể tính được độ dài của đoạn AD.
Độ dài đoạn đường AD là:
\(2345 + 4000 - 400 = 5945\,\left( m \right)\)
