Để phương trình sau có 4 nghiệm phân biệt: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) thì giá trị của tham số \(a\) là:
Trả lời bởi giáo viên
Xét phương trình: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) (1)
\( \Leftrightarrow a = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
Xét \(f\left( x \right) = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
\( = \left\{ \begin{array}{l}\left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 \ge 0\\ - \left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 < 0\end{array} \right.\)
\( = \left\{ \begin{array}{l} - 3{x^2} + 15x - 8 & {\rm{khi }}1 \le x \le 4\\{x^2} - 5x + 8 & {\rm{khi }}x \le 1 \vee x \ge 4\end{array} \right.\)
Bảng biến thiên:
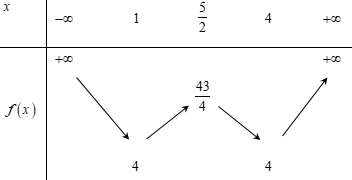
Dựa vào bảng biến thiên ta có phương trình (1) có 4 nghiệm phân biệt \( \Leftrightarrow 4 < a < \dfrac{{43}}{4}\).
Hướng dẫn giải:
- Cô lập \(a\) đưa về \(a = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
- Sử dụng phương pháp xét hàm số vế phải, lập bảng biến thiên suy ra giá trị của \(a\) để phương trình có \(4\) nghiệm.

