Để bất phương trình \(\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\) nghiệm đúng \(\forall x \in \left[ { - 5;3} \right]\), tham số \(a\) phải thỏa điều kiện:
Trả lời bởi giáo viên
\(\sqrt {\left( {x + 5} \right)\left( {3 - x} \right)} \le {x^2} + 2x + a \Leftrightarrow \sqrt { - {x^2} - 2x + 15} - {x^2} - 2x \le a\)
Đặt \(t = \sqrt { - {x^2} - 2x + 15} \), ta có bảng biến thiên
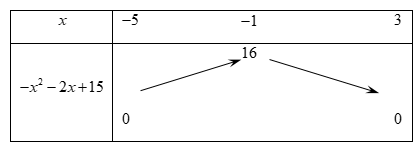
Suy ra \(t \in \left[ {0;4} \right]\).
Bất phương trình đã cho thành ${t^2} + t - 15 \le a$.
Xét hàm $f\left( t \right) = {t^2} + t - 15$ với \(t \in \left[ {0;4} \right]\)
Ta có bảng biến thiên
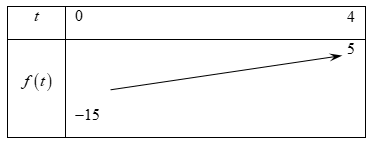
Bất phương trình \({t^2} + t - 15 \le a\) nghiệm đúng \(\forall t \in \left[ {0;4} \right]\) khi và chỉ khi \(a \ge 5.\)
Hướng dẫn giải:
- Đặt \(t = \sqrt { - {x^2} - 2x + 15} \), tìm điều kiện của \(t\) với chú ý \(x \in \left[ { - 5;3} \right]\), biến đổi về dạng \(a \ge f\left( t \right)\).
- Lập bảng biến thiên của hàm số \(f\left( t \right)\) trên đoạn \(D\) tìm được ở trên.
- Bất phương trình $f\left( t \right) \le a$ nghiệm đúng \(\forall t \in D\) khi và chỉ khi $a \ge \mathop {\max }\limits_D f\left( t \right)$.

