Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị?

Xét hàm số \(f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\) ta có

\(\begin{array}{l}f'\left( x \right) = 12{x^3} - 12{x^2} - 24x\\f'\left( x \right) = 0 \Leftrightarrow 12{x^3} - 12{x^2} - 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 1\\x = 2\end{array} \right.\end{array}\)

BBT:

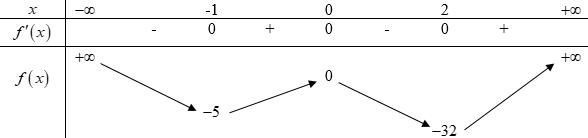
Ta có đồ thị \(y = f\left( x \right)\,\,\left( C \right)\) như sau:

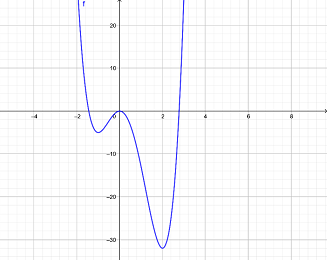
Để \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị thì:

TH1: \(\left( C \right)\) cắt đường thẳng \(y =  - m\) tại 2 điểm phân biệt khác cực trị

\( \Leftrightarrow \left[ \begin{array}{l} - m > 0\\ - 32 <  - m <  - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\5 < m < 32\end{array} \right.\)

Mà \(m \in {\mathbb{Z}^ + }\, \Rightarrow m \in \left\{ {6;7;...;31} \right\}\) : 26 giá trị.

TH2: \(\left( C \right)\) cắt đường thẳng \(y =  - m\) tại 3 điểm phân biệt, trong đó có 1 cực trị

\( \Leftrightarrow \left[ \begin{array}{l} - m = 0\\ - m =  - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\,(L)\\m = 5\,(TM)\end{array} \right.\)

Vậy, có tất cả 27 giá trị của m thỏa mãn.