Câu hỏi:
2 năm trước
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để phương trình \(y = \left| {{x^3} - 3x + m} \right|\) có 5 điểm cực trị?
Trả lời bởi giáo viên
Đáp án đúng: b
Để phương trình \(y = \left| {{x^3} - 3x + m} \right|\) có 5 điểm cực trị thì phương trình \({x^3} - 3x + m = 0\) có 3 nghiệm phân biệt.
Ta có: \({x^3} - 3x + m = 0\)\( \Leftrightarrow {x^3} - 3x = - m\).
Đặt \(f\left( x \right) = {x^3} - 3x \Rightarrow f'\left( x \right) = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\)
Bảng biến thiên:
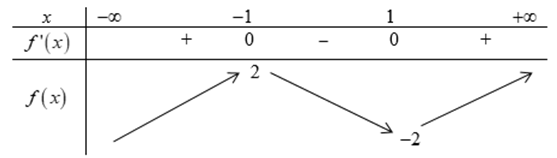
Dựa vào bảng biến thiên ta có \( - 2 < - m < 2 \Leftrightarrow - 2 < m < 2 \Rightarrow m \in \left\{ { - 1;0;1} \right\}\)
Hướng dẫn giải:
- Dựa vào số điểm cực trị để biện luận nghiệm của phương trình \(y = {x^3} - 3x + m\).
- Lập bảng biếb thiên và suy ra các giá trị của \(m.\)



