Có \(20g\) khí Heli chứa trong xilanh đậy kín bởi pittong biến đổi chậm từ \(\left( 1 \right) \to \left( 2 \right)\) theo đồ thị như hình vẽ:
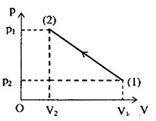
Cho \({V_1} = 30l,{p_1} = 5{\rm{a}}tm\) ; \({V_2} = 10l,{p_2} = 15{\rm{a}}tm\).Tìm nhiệt độ cao nhất mà khí đạt được trong quá trình trên?
Trả lời bởi giáo viên
Quá trình \(\left( 1 \right) - \left( 2 \right):p = aV + b\)
Thay các giá trị \(\left( {{p_1},{V_1}} \right)\) và \(\left( {{p_2},{V_2}} \right)\) vào \(\left( 1 \right)\) ta được:
\(\left\{ \begin{array}{l}5 = 30{\rm{a}} + b{\rm{ }}\left( 1 \right)\\10 = 10{\rm{a}} + b{\rm{ }}\left( 2 \right)\end{array} \right.\)
Từ\(\left( 1 \right)\) và \(\left( 2 \right)\)suy ra: \(\left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 20\end{array} \right. \to p = - \frac{V}{2} + 20\)
Ta suy ra: \(pV = - \frac{{{V^2}}}{2} + 20V{\rm{ }}\left( 3 \right)\)
Mặt khác: \(pV = \frac{m}{M}RT = \frac{{20}}{4}RT = 5{\rm{R}}T{\rm{ }}\left( 4 \right)\)
Từ \(\left( 4 \right)\), ta suy ra: \(T = - \frac{{{V^2}}}{{10{\rm{R}}}} + \frac{{4V}}{R}{\rm{ }}\left( 5 \right)\)
Xét hàm \(T = f\left( V \right)\) (phương trình số 5), ta có:
\(T = {T_{{\rm{max}}}}\)khi \(V = - \frac{b}{{2{\rm{a}}}} = - \frac{{\frac{4}{R}}}{{2.\frac{{ - 1}}{{10{\rm{R}}}}}} = 20l\)
Khi đó: \({T_{max}} = - \frac{{{{20}^2}}}{{10.0,082}} + \frac{{4.20}}{{0,082}} = 487,8K\)
Hướng dẫn giải:
Đọc đồ thị V-T
Xác định các quá trình