Trả lời bởi giáo viên
Đáp án đúng: a
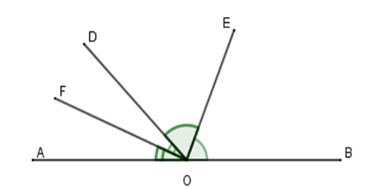
Giả sử \(\widehat {AOD}\) và \(\widehat {DOB}\) là hai góc kề bù, \(OE\) là phân giác \(\widehat {DOB}\) và \(OF\) là phân giác \(\widehat {DOA}.\)
Ta có \(\widehat {AOD} + \widehat {BOD} = 180^\circ \) (tính chất hai góc kề bù)
Vì \(OE\) là phân giác \(\widehat {DOB}\) nên \(\widehat {BOE} = \widehat {EOD} = \dfrac{{\widehat {DOB}}}{2}\,\,\,\left( 1 \right)\)
Vì \(OF\) là phân giác \(\widehat {DOA}\) nên \(\widehat {AOF} = \widehat {DOF} = \dfrac{{\widehat {AOD}}}{2}\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {DOF} + \widehat {DOE} = \dfrac{{\widehat {DOA}}}{2} + \dfrac{{\widehat {DOB}}}{2}\) \( = \dfrac{{\widehat {DOA} + \widehat {DOB}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ \)
Hay \(\widehat {EOF} = 90^\circ \Rightarrow OE \bot OF\) . Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau.
Hướng dẫn giải:
Áp dụng tính chất hai góc kề bù và tính chất tia phân giác của một góc.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
