Cho tam giác $ABC$ có trực tâm $H$, trọng tâm $G$ và tâm đường tròn ngoại tiếp $O$ . Phép vị tự tâm $G$ biến $H$ thành $O$ có tỉ số là :
Trả lời bởi giáo viên
Gọi $H$ và $O$ lần lượt là trực tâm và tam đường tròn ngoại tiếp tâm giác $ABC$ .
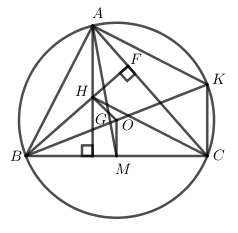
Gọi $M$ là trung điểm của $BC$ , kẻ đường kính $BK$.
Xét đường tròn ngoại tiếp tâm $O$ có \(\widehat {BCK}\) nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {BCK} = {90^0} \Rightarrow BC \bot CK\)
Mà \(AH \bot BC \Rightarrow AH//CK\)
Tương tự ta chứng minh được \(AK//CH\)
\( \Rightarrow \) Tứ giác $AHCK$ là hình bình hành \( \Rightarrow AH = CK\)
Có $OM$ là đường trung bình của tam giác \(BCK \Rightarrow OM//CK//AH\) và \(OM = \dfrac{1}{2}CK = \dfrac{1}{2}AH\).
Gọi \(G = AM \cap OH\) ta dễ thấy \(\Delta AGH \sim \Delta MGO\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{AG}}{{MG}} = \dfrac{{AH}}{{OM}} = 2 = \dfrac{{HG}}{{OG}}\) , mà $AM$ là trung tuyến của tam giác \(ABC \Rightarrow G\) là trọng tâm tam giác $ABC$ . Vậy $H,G,O$ thẳng hàng, với $G$ là trọng tâm tam giác $ABC$ và \(\dfrac{{HG}}{{OG}} = 2 \Rightarrow \overrightarrow {GO} = - \dfrac{1}{2}\overrightarrow {GH} \)
\( \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( H \right) = O\).
Hướng dẫn giải:
Chứng minh $H,G,O$ thẳng hàng mà tìm mối tỉ số \(\dfrac{{GO}}{{GH}}\)

