Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có \(\widehat A = {90^0}\), tia phân giác $BD$ của góc $B$ (\(D \in AC\)). Trên cạnh $BC$ lấy điểm $E$ sao cho $BE = BA.$ Hai góc nào sau đây bằng nhau?
Trả lời bởi giáo viên
Đáp án đúng: c
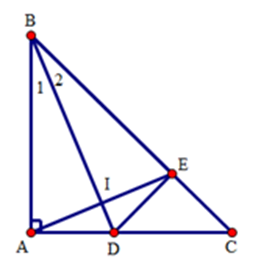
Xét hai tam giác $BDA$ và $BDE$ có:$BA = BE\left( {gt} \right),$ \(\widehat {{B_1}} = \widehat {{B_2}}\) (do $BD$ là tia phân giác của góc B);
$BD$ là cạnh chung. Suy ra \(\Delta BDA = \Delta BDE\) (c.g.c)
Suy ra \(\widehat {BED} = \widehat {BAD} = {90^ \circ }\) (hai góc tương ứng)
Trong các tam giác $ABC$ và $EDC$ vuông ở $A$ và $E,$ ta có:
\(\widehat {ABC} + \widehat C = {90^ \circ }\) và \(\widehat {EDC} + \widehat C = {90^ \circ }\), suy ra \(\widehat {EDC} = \widehat {ABC}\).
Hướng dẫn giải:
Sử dụng trường hợp bằng nhau thứ hai của tam giác để suy ra \(\widehat {BED} = \widehat {BAD} = 90^\circ \) và lập luận để chỉ ra \(\widehat {EDC} = \widehat {ABC}.\)
Câu hỏi khác
- Đề kiểm tra 15 phút chương 6: Tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: Tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: Tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: Tam giác - đề số 2 Toán 7 có lời giải chi tiết
