Cho phản ứng hạt nhân \(_0^1n + _3^6Li \to _1^3H + \alpha \). Hạt Li đứng yên, nơtron có động năng \(2MeV\). Hạt \(\alpha \) và hạt nhân H bay ra theo các hướng hợp với hướng tới của nơtron những góc tương ứng bằng \({15^0}\)  và \({30^0}\). Bỏ qua búc xạ gamma. Lấy tỉ số khối lượng các hạt bằng tỉ số giữa các số khối của chúng. Phản ứng thu hay tỏa bao nhiêu năng lượng?

Phương trình phản ứng là: \(_0^1n + _3^6Li \to _1^3H + _2^4He\)

Áp dụng định luật bảo toàn động lượng, ta vẽ được giản đồ vecto động lượng của phản ứng là:

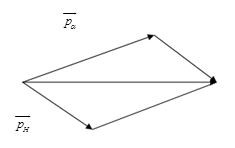
Áp dụng định lý hàm số sin trong tam giác ta có:

\(\begin{array}{l}\dfrac{{{p_n}}}{{\sin {{135}^0}}} = \dfrac{{{p_H}}}{{\sin {{15}^0}}} = \dfrac{{{p_\alpha }}}{{\sin {{30}^0}}}\\ =  > \dfrac{{{p_H}}}{{{p_n}}} = \dfrac{{\sin {{15}^0}}}{{\sin {{135}^0}}} =  > \dfrac{{{p_H}^2}}{{{p_n}^2}} = \dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}}\\ =  > \dfrac{{{m_H}.{K_H}}}{{{m_n}.{K_n}}} = \dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}}\\ =  > {K_H} = \dfrac{{1.2}}{3}.\dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}} = 0,089MeV\\\dfrac{{{p_{He}}}}{{{p_n}}} = \dfrac{{\sin {{30}^0}}}{{\sin {{135}^0}}} =  > \dfrac{{{p_{He}}^2}}{{{p_n}^2}} = \dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}}\\ =  > \dfrac{{{m_{He}}.{K_{He}}}}{{{m_n}.{K_n}}} = \dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}}\\ =  > {K_{He}} = \dfrac{{1.2}}{4}.\dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}} = 0,25MeV\end{array}\)

Năng lượng thu vào  \(\Delta E = {K_{tr}} - {K_s} = 2 - 0,089 - 0,25 = 1,66MeV\)