Câu hỏi:
2 năm trước
Cho một nguồn điểm phát sóng âm tại điểm O trong môi trường đẳng hướng và không hấp thụ âm. Hai điểm A, B tạo thành tam giác vuông tại O, cách O lần lượt là 12 m và 15 m. Cho một máy thu di chuyển trên đoạn thẳng AB. Độ chênh giữa mức cường độ âm lớn nhất và nhỏ nhất trong quá trình di chuyển giữa hai điểm A, B là
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có hình vẽ:
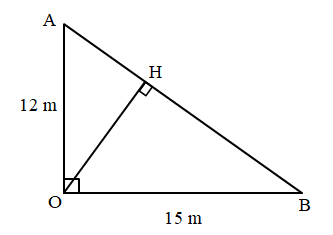
Ta có cường độ âm: \(I = \dfrac{P}{{4\pi {r^2}}} \Rightarrow I \sim \dfrac{1}{{{r^2}}}\)
→ Mức cường độ âm lớn nhất khi máy thu ở tại H, mức cường độ âm nhỏ nhất khi máy thu tại B
Do ∆ABC vuông tại O, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} = {12^2} + {15^2} \Rightarrow AB = \sqrt {369} = 3\sqrt {41} \,\,\left( m \right)\\OH = \dfrac{{OA.OB}}{{AB}} = \dfrac{{12.15}}{{3\sqrt {41} }} = \dfrac{{60}}{{\sqrt {41} }}\,\,\left( m \right)\end{array}\)
Hiệu mức cường độ âm tại M và B là:
\({L_H} - {L_B} = 10\lg \dfrac{{{I_H}}}{{{I_B}}} = 10\lg \dfrac{{O{B^2}}}{{O{H^2}}} = 10\lg \dfrac{{{{15}^2}}}{{{{\left( {\dfrac{{60}}{{\sqrt {41} }}} \right)}^2}}} \approx 4,1\,\,\left( {dB} \right)\)
Hướng dẫn giải:
Cường độ âm: \(I = \dfrac{P}{{4\pi {r^2}}}\)
Hiệu hai mức cường độ âm: \({L_A} - {L_B}\left( {dB} \right) = 10\lg \dfrac{{{I_A}}}{{{I_B}}} = 10\lg \dfrac{{O{B^2}}}{{O{A^2}}}\)
Câu hỏi khác
- Đề thi thử thpt qg sở gdđt hà nội - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt chuyên lam sơn - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg sở gdđt kiên giang - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 01 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt kim liên (2021) Lý 12 có lời giải chi tiết
