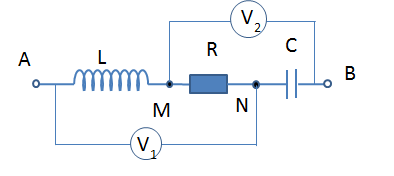
Cho mạch điện xoay chiều như hình vẽ, cuộn dây thuần cảm. Số chỉ các vôn kế ${V_1},{\rm{ }}{V_2}$ lần lượt là ${U_1} = {\rm{ }}30V$; ${U_2} = 40V$. Biết hiệu điện thế tức thời ${u_{AN}}$ biến thiên lệch pha $\dfrac{\pi }{2}$ với hiệu điện thế tức thời ${u_{MB}}$. Hiệu điện thế hiệu dụng ở hai đầu điện trở thuần là:

Ta có: ${U_{RL}} \bot {U_{RC}} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1 \to \dfrac{{{Z_L}}}{R}\dfrac{{{Z_C}}}{R} = 1 \to {U_L}{U_C} = U_R^2$

$\left\{ \begin{array}{l}U_R^2 + U_L^2 = {30^2}(1)\\U_R^2 + U_C^2 = {40^2}(2)\end{array} \right.$

Lấy:

$\begin{array}{l}(1) + (2)\\ \leftrightarrow 2U_R^2 + U_L^2 + U_C^2 = {30^2} + {40^2}\\ \leftrightarrow 2U_R^2 + {\left( {{U_L} + {U_C}} \right)^2} - 2{U_L}{U_C} = {30^2} + {40^2}\\ \to {\left( {{U_L} + {U_C}} \right)^2} = 2500\\ \to \left( {{U_L} + {U_C}} \right) = 50\end{array}$

Lấy:

$\begin{array}{l}\left( 2 \right) - \left( 1 \right)\\ \leftrightarrow U_C^2 - U_L^2 = {40^2} - {30^2}\\ \leftrightarrow \left( {{U_C} + {U_L}} \right)\left( {{U_C} - {U_L}} \right) = {40^2} - {30^2}\\ \to \left( {{U_C} - {U_L}} \right) = \dfrac{{{{40}^2} - {{30}^2}}}{{50}} = 14\\ \to \left\{ \begin{array}{l}{U_L} = 18V\\{U_C} = 32V\end{array} \right.\\ \to {U_R} = \sqrt {{{30}^2} - {{18}^2}}  = 24V\end{array}$