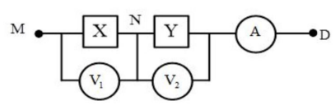
Cho mạch điện như hình vẽ: X, Y là hai hộp kín, mỗi hộp chỉ chứa hai trong ba phần tử sau: điện trở thuần, cuộn cảm thuần và tụ điện, hai phần tử được mắc nối tiếp. Các vôn kế và ampe lý tưởng có thể đo được dòng một chiều và dòng xoay chiều. Ban đầu, măc hai điểm N, D vào hai cực của nguồn điện một chiều không đổi thì V2 chỉ 45V, ampe kế chỉ 1,5A. Sau đó, ngắt ND khỏi nguồn, mắc M, D vào hai cực của nguồn điện xoay chiều có điện áp \(u = 120\cos 100\pi t\left( V \right)\) thì ampe kế chỉ 1,0 A, số chỉ hai vôn kế bằng nhau nhưng điện áp tức thời hai đầu vôn kế lệch pha nha\(\frac{\pi }{2}\). Kết luận nào sau đây là sai:
Trả lời bởi giáo viên
\({R_Y} = \frac{{45}}{{1,5}} = 30\Omega \)
\(Z = \frac{U}{I} = \frac{{60\sqrt 2 }}{1} = 60\sqrt 2 = \sqrt {{R^2} + Z_L^2} \Rightarrow {Z_L} = 30\sqrt 7 \Omega \)
+ Y chứa R, L với \({R_Y} = \frac{{45}}{{1,5}} = 30\Omega \)
+ \({u_X} \bot {u_Y}\) => X chứa R và C => C đúng.
\(\tan {\varphi _X}.\tan {\varphi _Y} = - 1 \Leftrightarrow - \frac{{{Z_C}}}{R}.\frac{{{Z_Y}}}{R} = - 1 \Leftrightarrow {Z_L}.{Z_C} = {R_X}.{R_Y} = 900\)
+) \(R_X^2 + Z_L^2 = {30^2} + Z_L^2\)
\({\left( {{R_X} + {R_Y}} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {60\sqrt 2 } \right)^2} = 7200\)
=> Mạch có hai điện trở và các điện trở này có giá trị khác nhau => D đúng.
+ Ta có:
\(u_X^2 + u_Y^2 = {u^2} \Leftrightarrow u_X^2 = u_Y^2 = \frac{{{u^2}}}{2}\)
\( \Rightarrow {U_X} = {U_Y} = \frac{U}{{\sqrt 2 }} = \frac{{60\sqrt 2 }}{{\sqrt 2 }} = 60\left( V \right)\)
\( \Rightarrow Z_L^2 + {30^2} = {60^2} = 3600 \Leftrightarrow {Z_L} = 30\sqrt 3 \)
Lại có:
\({Z_L}.{Z_C} = {R_X}.{R_Y} \Leftrightarrow 30\sqrt 3 .{Z_C} = {R_X}.30 \Leftrightarrow {R_X} = {Z_C}\sqrt 3 \)
\({Z_X} = 2{{\rm{Z}}_C} = 60 \Leftrightarrow {Z_C} = 30 \Leftrightarrow C = \frac{{{{10}^{ - 3}}}}{{3\pi }}\left( F \right)\) => A đúng
Câu hỏi khác
- Đề thi thử khoa học tự nhiên - lần 1 Tự chọn Đánh giá năng lực có lời giải chi tiết
- Đề thi thử khoa học tự nhiên - đhbk - lần 2 Tự chọn Đánh giá năng lực có lời giải chi tiết
- Đề thi thử khoa học tự nhiên - đề số 1 Tự chọn Đánh giá tư duy đại học Bách Khoa Hà Nội có lời giải chi tiết
- Đề thi thử khoa học tự nhiên - đề số 2 Tự chọn Đánh giá tư duy đại học Bách khoa Hà Nộicó lời giải chi tiết
- Đề thi khoa học tự nhiên - đề số 4 Tự chọn Đánh giá năng lực có lời giải chi tiết
