Cho khối tứ diện \(ABCD\). Gọi \(M,N,E\) lần lượt là trung điểm của \(AB,BD,DA\). Tỉ số \(\dfrac{{{V_{MNEC}}}}{{{V_{ABCD}}}}\)=?
Trả lời bởi giáo viên
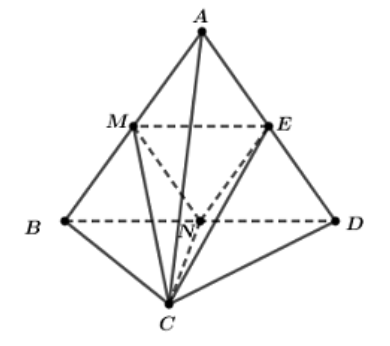
Ta có: \({V_{ABCD}} = {V_{C.ABD}} = \dfrac{1}{3}{S_{ABD}}.d\left( {C,\left( {ABD} \right)} \right)\)
\({V_{MNEC}} = {V_{C.MNE}} = \dfrac{1}{3}{S_{MNE}}.d\left( {C,\left( {MNE} \right)} \right) = \dfrac{1}{3}{S_{MNE}}.d\left( {C,\left( {ABD} \right)} \right)\)
\( \Rightarrow \dfrac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \dfrac{{\dfrac{1}{3}{S_{MNE}}.d\left( {C,\left( {ABD} \right)} \right)}}{{\dfrac{1}{3}{S_{ABD}}.d\left( {C,\left( {ABD} \right)} \right)}} = \dfrac{{{S_{MNE}}}}{{{S_{ABD}}}}\)
Dễ thấy \(\Delta MNE\) đồng dạng \(\Delta DAB\) theo tỉ số \(\dfrac{1}{2}\) nên \(\dfrac{{{S_{MNE}}}}{{{S_{ABD}}}} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\)
Vậy \(\dfrac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \dfrac{{{S_{MNE}}}}{{{S_{ABD}}}} = \dfrac{1}{4}\)
Hướng dẫn giải:
- Tính thể tích khối tứ diện \(MNEC\) và \(ABCD\).
- So sánh diện tích đáy và chiều cao mỗi khối tứ diện và suy ra tỉ số.



