Câu hỏi:
2 năm trước
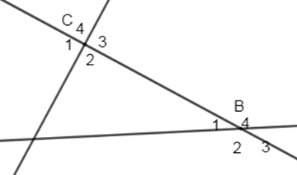
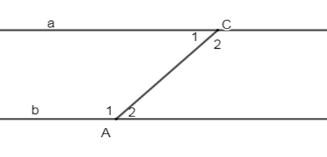
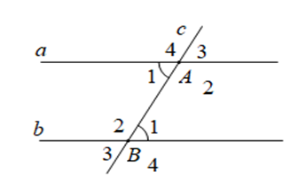
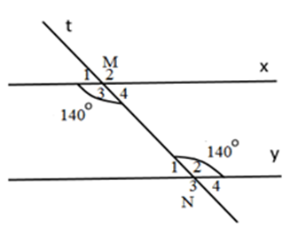
Cho hình vẽ sau:
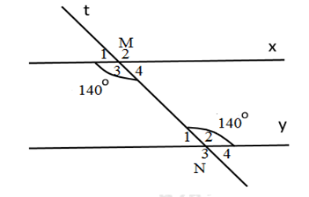
Biết \(\widehat {{M_3}} = \widehat {{N_2}} = {140^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_2}},\,\widehat {{M_3}} + \widehat {{N_1}}.\)
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{M_4}} = {180^0} - \widehat {{M_3}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_4}} + \,\widehat {{N_2}} = {40^0} + {140^0} = {180^0}\end{array}\)
Ta có: \(\widehat {{N_2}} + \widehat {{N_1}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{N_1}} = {180^0} - \widehat {{N_2}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_3}} + \widehat {{N_1}} = {140^0} + {40^0} = {180^0}\end{array}\)
Hướng dẫn giải:
Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\).
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
