Cho hình hộp chữ nhật $ABCD.EFGH.$ Chọn câu đúng:

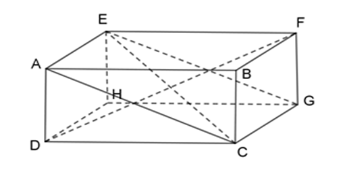
+ ) Ta có: $AE//CG,\;A{\rm{E}} = CG\;(gt)$

Suy ra tứ giác ACGE là hình bình hành.

Mặt khác: $A{\rm{E}} \bot mp(EFGH)$

Mà $EG \subset mp(EFGH) \Rightarrow AE \bot EG\;$tại $E.$

Vậy tứ giác $ACGE$ là hình chữ nhật nên $A$ đúng.

+) Vì $DH \bot mp(EFGH)$ nên $DH \bot HF$ tại $H.$

Áp dụng định lý Pitago cho tam giác $DHF$ vuông tại $H,$ ta có: $D{H^2} + H{F^2} = D{F^2}\;(1)$

Vì $A{\rm{E}} \bot mp(ABC{\rm{D}})$ nên $A{\rm{E}} \bot AC$ tại $A.$

Áp dụng định lý Pitago cho tam giác EAC vuông tại A, ta có: $E{{\rm{A}}^2} + A{C^2} = E{C^2}\;(2)$

Mà DH = AE; HF = EG = AC (Hai đường chéo của hình chữ nhật) (3)

Từ (1), (2), (3) suy ra: $D{F^2} = E{C^2} \Rightarrow DF = CE\;$nên B đúng.