Cho hình hộp chữ nhật ABCD.A′B′C′D′ có \(AB = a\sqrt 2 ,BC = 2a,AA' = a\sqrt 3 \). Gọi \(\alpha \) là góc giữa hai mặt phẳng (ACD′) và (ABCD) (tham khảo hình vẽ dưới đây).
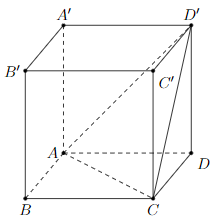
Giá trị tanα bằng
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
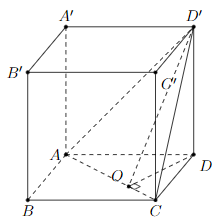
Kẻ DO\( \bot \)AC.
Ta có: \(DD' \bot \left( {ABCD} \right) \Rightarrow DD' \bot AC\)
\( \Rightarrow AC \bot \left( {ODD'} \right)\)
Suy ra \(AC \bot D'O\)
Do đó \(\widehat {\left( {\left( {ACD'} \right),\left( {ABCD} \right)} \right)} = \widehat {\left( {D'O,DO} \right)}\)\( = \widehat {D'OD} = \alpha \)
Xét tam giác ACD vuông tại D, đường cao DO có:
\(\dfrac{1}{{D{O^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{C{D^2}}} = \dfrac{1}{{4{a^2}}} + \dfrac{1}{{2{a^2}}} = \dfrac{3}{{4{a^2}}}\)
Suy ra \(DO = \dfrac{{2a}}{{\sqrt 3 }}\)
Tam giác DD’O vuông tại D, ta có: \(\tan \alpha = \dfrac{{DD'}}{{DO}} = \dfrac{{a\sqrt 3 }}{{\dfrac{{2a}}{{\sqrt 3 }}}} = \dfrac{3}{2}\)
Hướng dẫn giải:
- Kẻ DO\( \bot \)AC.
- Xác định góc giữa (ACD′) và (ABCD)
- Tính tan góc giữa (ACD′) và (ABCD)



