Câu hỏi:
3 năm trước
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy góc \({60^\circ }\). Hình nón có đỉnh \(S\), đáy là đường tròn ngoại tiếp tứ giác $A B C D$ có diện tích xung quanh là
Trả lời bởi giáo viên
Đáp án đúng: b
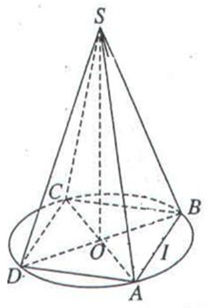
Gọi \(O\) là tâm của đáy \(ABCD; \;SO\bot (ABCD)\).
Góc giữa cạnh bên và đáy là góc \(\widehat {SDO} = {60^0}\)
Mà $OD=\dfrac{a}{\sqrt{2}}$
\( \Rightarrow l = SD =2OD=a\sqrt 2\)
Diện tích xung quanh hình nón cần tính là
\({S_{xq}} = \pi rl = \pi .DO \cdot l =\pi .a\sqrt 2 . \dfrac{{a}}{\sqrt 2}=\pi .a^2\)
Hướng dẫn giải:
- Gọi \(O\) là tâm của đáy \(ABCD; \;SO\bot (ABCD)\).
- Tính OD và SD
- Tính \({S_{xq}} = \pi rl \)


