Cho hình chóp tứ giác đều $S . A B C D$ có cạnh đáy bằng \(a\), cạnh bên hợp với đáy một góc \({60^\circ }\). Gọi \(M\) là điểm đối xứng của \(C\) qua $D, N$ là trung điểm $S C$. Mặt phẳng \((BMN)\) chia khối chóp $S . A B C D$ thành 2 phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:
Trả lời bởi giáo viên
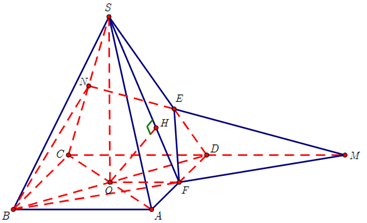
Giả sử các điểm như hình vẽ.
\(E = SD \cap MN \Rightarrow E\) là trọng tâm tam giác \(SCM,DF//BC \Rightarrow F\) là trung điềm $B M$.
Ta có: \((\widehat {SD,(ABCD)}) = \widehat {SDO} = {60^\circ } \Rightarrow SO = \dfrac{{a\sqrt 6 }}{2},SF = \sqrt {S{O^2} + O{F^2}} = \dfrac{{a\sqrt 7 }}{2}\)
\( \Rightarrow d(O,(SAD)) = OH = h = \dfrac{{a\sqrt 6 }}{{2\sqrt 7 }};{S_{SAD}} = \dfrac{1}{2}SF \cdot AD = \dfrac{{{a^2}\sqrt 7 }}{4}\)
\(\dfrac{{{V_{MEFD}}}}{{{V_{MNBC}}}} = \dfrac{{ME}}{{MN}} \cdot \dfrac{{MF}}{{MB}} \cdot \dfrac{{MD}}{{MC}} = \dfrac{1}{6}\)
\( \Rightarrow {V_{BFDCNE}} = \dfrac{5}{6}{V_{MNBC}} = \dfrac{5}{6} \cdot \dfrac{1}{3} \cdot d(M,(SAD)) \cdot \dfrac{1}{2}{S_{SBC}} = \dfrac{5}{{18}} \cdot 4h \cdot \dfrac{1}{2}{S_{SAD}} = \dfrac{{5{a^3}\sqrt 6 }}{{72}}\)
\({V_{S.ABCD}} = \dfrac{1}{3}SO \cdot {S_{ABCD}} = \dfrac{{{a^3}\sqrt 6 }}{6} \Rightarrow {V_{SABFEN}} = {V_{S.ABCD}} - {V_{BFDCNE}} = \dfrac{{7{a^3}\sqrt 6 }}{{36}}\).
Suy ra: \(\dfrac{{{V_{SABFEN}}}}{{{V_{BFDCNE}}}} = \dfrac{7}{5}\).
Hướng dẫn giải:
\({V_{SABFEN}} = {V_{S.ABCD}} - {V_{BFDCNE}}\)
\({V_{BFDCNE}} = \dfrac{5}{6}{V_{MNBC}}\)


