Cho hình chóp tứ giác đều có cạnh đáy dài $16cm$  và trung đoạn dài $20cm.$  Tính thể tích hình chóp. (làm tròn đến hàng phần trăm)

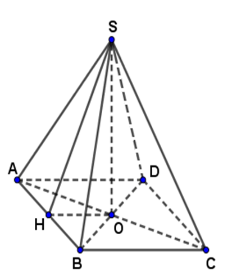
Xét hình chóp tứ giác đều $S.ABCD\;$  có đáy là hình vuông cạnh $16cm$. 
$SO$ là đường cao; $SH$  là trung đoạn $(H \in AB)$
Vì $SAB$ là tam giác cân nên $H$  là trung điểm của $AB$.

$O$  là giao điểm của hai đường chéo trong hình vuông $ABCD$  nên $O$  là trung điểm $AC$  
Do đó, $HO$  là đường trung bình trong tam giác $ABC,$  suy ra $HO = \dfrac{1}{2}BC = 8(cm)$  
Xét tam giác $SHO$  vuông tại $O,$  
Áp dụng định lý Pytago, ta có:
$S{H^2} = H{O^2} + S{O^2}$$ \Rightarrow SO^2 = S{H^2} - H{O^2}$  $ \Rightarrow SO = \sqrt {400 - 64}  = 4\sqrt {21} (cm)$

Vậy thể tích hình chóp $S.ABCD\;$  là 
$V=\dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.4\sqrt {21} {.16^2} \approx 1564,19\,\left( {c{m^3}} \right)$