Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
Trả lời bởi giáo viên
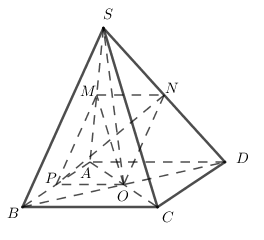
Dễ dàng chứng minh được $MNOP $ là hình bình hành \( \Rightarrow M,N,O,P\) đồng phẳng \( \Rightarrow A,C\) sai.
Ta có : $MN$ là đường trung bình của tam giác $SAD$ \( \Rightarrow MN//AD//BC\)
$ON$ là đường trung bình của tam giác $SBD$ \( \Rightarrow ON//SB\)
\( \Rightarrow (MON) // (SBC)\)
\( \Rightarrow \) Đáp án B đúng.
Đáp án D sai vì \(N \in \left( {MNP} \right) \cap \left( {SBD} \right)\)
Hướng dẫn giải:
\(\left\{ \begin{array}{l}a//\left( \beta \right)\\b//\left( \beta \right)\\a \cap b \subset \left( \alpha \right)\end{array} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\) hoặc \(\left\{ \begin{array}{l}a//a'\\b//b'\\a \cap b \subset \left( \alpha \right)\\a',b' \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\)

