Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm \(AD\) và \(BC.\) Giao tuyến của hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) là:
Trả lời bởi giáo viên
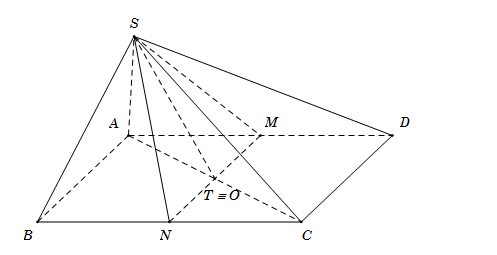
\( \bullet \) \(S\)là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)
\( \bullet \) Gọi \(O = AC \cap BD\) là tâm của hình hình hành.
Trong mặt phẳng \(\left( {ABCD} \right)\) gọi \(T = AC \cap MN\) $ \Rightarrow T \equiv O$
\( \Rightarrow \left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in MN \subset \left( {SMN} \right) \Rightarrow O \in \left( {SMN} \right)\end{array} \right. \)
\(\Rightarrow O\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)
Vậy \(\left( {SMN} \right) \cap \left( {SAC} \right) = SO.\)
Hướng dẫn giải:
- Tìm điểm chung dễ thấy của hai mặt phẳng.
- Tìm điểm chung thứ hai bằng cách tìm hai đường thẳng lần lượt thuộc hai mặt phẳng mà chúng cắt nhau.

