Câu hỏi:
2 năm trước
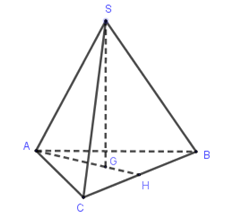
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và \(SA = SB = SC = b\). Gọi \(G\) là trọng tâm \(\Delta ABC\). Độ dài \(SG\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
Theo bài ra hình chóp \(S.ABC\) là hình chóp tam giác đều.
Gọi \(H\) là trung điểm của \(BC\), ta có \(SG \bot (ABC),G \in AH\).
Mà \(AH = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AG = \dfrac{2}{3}AH = \dfrac{{a\sqrt 3 }}{3}\).
Tam giác \(SAG\) vuông tại \(G\) nên theo định lý Pi-ta-go ta có :
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{3}} = \sqrt {\dfrac{{3{b^2} - {a^2}}}{3}} = \dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}\)
Hướng dẫn giải:
- Sử dụng tính chất hình chóp đều: Hình chiếu của đỉnh lên mặt đáy là trọng tâm của tam giác đáy.
- Từ đó tính được độ dài \(SG\) dựa vào mối quan hệ giữa cạnh và góc trong tam giác vuông.
Câu hỏi khác
- Bài tập phần hai đường thẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần góc giữa đường thẳng và mặt phẳng thi ĐGTD Bách khoa
- Bài tập phần hai mặt phẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần đường thẳng vuông góc với mặt phẳng thi ĐGTD Bách khoa
- Bài tập góc giữa hai mặt phẳng môn toán ĐGNL có lời giải
