Câu hỏi:
2 năm trước
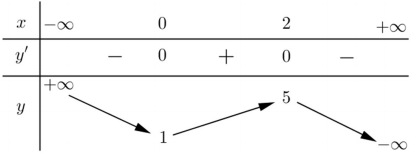
Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình \(f\left( {\sin x} \right) = m\) có nghiệm thuộc khoảng \(\left( {0;\pi } \right)\) là
Trả lời bởi giáo viên
Đáp án đúng: d
Đặt \(\sin x = t\). Với \(x \in \left( {0;\pi } \right) \Rightarrow t \in \left( {0;1} \right]\).
Khi đó phương trình ban đầu trở thành \(f\left( t \right) = m\) có nghiệm \(t \in \left( {0;1} \right]\).
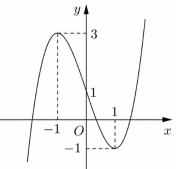
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và \(y = m\).
Dựa vào đồ thị hàm số ta thấy, để phương trình \(f\left( t \right) = m\) có nghiệm \(t \in \left( {0;1} \right]\)\( \Rightarrow m \in \left[ { - 1;1} \right)\).
Hướng dẫn giải:
+) Đặt \(t = \sin x\), dựa vào khoảng giá trị của x xác định khoảng giá trị của t.
+) Cô lập m, đưa phương trình về dạng \(f\left( t \right) = m\), khi đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và \(y = m\).
Giải thích thêm:
Sau khi đặt ẩn phụ \(t = \sin x\), nhiều học sinh xác định sai khoảng giá trị của t, nên biểu diễn trên đường tròn lượng giác để thu được kết quả đúng nhất.
