Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
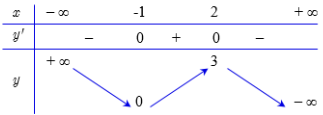
Số điểm cực đại và cực tiểu của hàm số \(y = {f^2}\left( {2x} \right) - 2f\left( {2x} \right) + 1\) lần lượt là
Trả lời bởi giáo viên
Ta có:
\(\begin{array}{l}y' = 2f\left( {2x} \right).f'\left( {2x} \right).2 - 4f'\left( {2x} \right) = 4f'\left( {2x} \right)\left[ {f\left( {2x} \right) - 1} \right]\\y' = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( {2x} \right) = 0\\f\left( {2x} \right) = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = - 1\\2x = 2\\2x = a \in \left( { - \infty ; - 1} \right)\\2x = b \in \left( { - 1;2} \right)\\2x = c \in \left( {2; + \infty } \right)\end{array} \right.\end{array}\)
Ta có bảng xét dấu đạo hàm của hàm số \(y = {f^2}\left( {2x} \right) - 2f\left( {2x} \right) + 1\) là:
Ta thấy y’ có ba lần đổi dấu từ âm sang dương, hai lần đổi dấu từ dương sang âm.
Vậy hàm số \(y = {f^2}\left( {2x} \right) - 2f\left( {2x} \right) + 1\) có hai điểm cực đại và 3 điểm cực tiểu.
Hướng dẫn giải:
- Tính $y’$ và giải \(y' = 0\)
- Lập bảng xét dấu đạo hàm của hàm số \(y = {f^2}\left( {2x} \right) - 2f\left( {2x} \right) + 1\)
- Tìm số cực đại và số cực tiểu.
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
