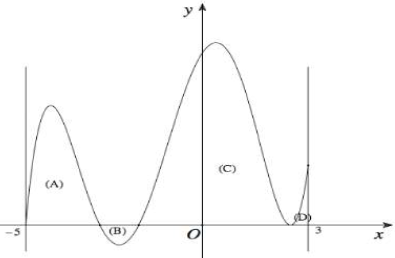
Cho hàm số \(f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ { - 5;3} \right]\) có đồ thị như hình vẽ bên. Biết diện tích của hình phẳng \(\left( A \right),\left( B \right),\left( C \right),\left( D \right)\) giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và trục hoành lần lượt là 6; 3; 12; 2. Tính tích phân \(\int\limits_{ - 3}^1 {\left[ {2f\left( {2x + 1} \right) + 1} \right]dx} \) bằng

Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b

Đáp án:

Tính tổng tất cả các nghiệm của phương trình \((2\cos 2x + 5)\left( {{{\sin }^4}x - {{\cos }^4}x} \right) + 3 = 0\) trên khoảng \((0;2\pi )\).

Mặt sàn tầng trệt ngôi nhà cao hơn mặt sân \(0,4\;{\rm{m}}\). Cầu thang đi tầng trệt lên tầng hai có 51 bậc, mỗi bậc cao \(22\;{\rm{cm}}\). Độ cao của tầng hai so với mặt sân là:

Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là 0,6 . Người đó bắn hai viên đạn một cách độc lập. Xác suất để một viên đạn bắn trúng mục tiêu và một viên đạn bắn trượt mục tiêu là:

Trong một nông trường chăn nuôi bò sữa ta thu nhập được số liệu sau:

Số con bò cho sản lượng sữa hàng ngày thấp nhất của nông trường là bao nhiêu ?

Một cái cổng hình parabol có dạng \(y =  - \frac{1}{2}{x^2}\) có chiều rộng \(d = 4m.\)

Tính chiều cao \(h\) của cổng (xem hình minh họa)

Với những giá trị nào của \(m\) thì đường thẳng \(\left( \Delta  \right):\,\,3x + 4y + 3 = 0\) tiếp xúc với đường tròn \(\left( C \right):\,\,{(x - m)^2} + {y^2} = 9\)?