Câu hỏi:
2 năm trước
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau
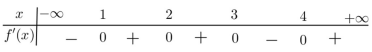
Hàm số \(y = 3f\left( {x + 2} \right) - {x^3} + 3x\) đồng biến trên khoảng nào dưới đây ?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có : \(y = 3f\left( {x + 2} \right) - {x^3} + 3x\) \( \Rightarrow y' = 3f'\left( {x + 2} \right) - 3{x^2} + 3\).
Xét \(\, - 1 < x < 0\) ta có :
\(\left\{ \begin{array}{l}1 < x + 2 < 2 \Rightarrow f'\left( {x + 2} \right) > 0\\{x^2} < 1 \Leftrightarrow {x^2} - 1 < 0\end{array} \right. \) \(\Rightarrow 3f'\left( {x + 2} \right) - 3{x^2} + 3 > 0\,\,\forall x \in \left( {-1;0} \right)\).
Vậy hàm số đã cho đồng biến trên \(\left( { - 1;0} \right)\).
Hướng dẫn giải:
Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {a;b} \right)\) khi và chỉ khi \(f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm.
Lưu ý công thức tính đạo hàm của hàm hợp. Sau đó thử từng đáp án để chọn kết quả đúng.
