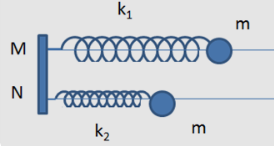
Cho hai con lắc lò xo nằm ngang \((k_1, m)\) và \((k_2, m)\) như hình vẽ. Trục dao động M và N cách nhau \(9cm\). Lò xo \(k_1\) có độ cứng \(100 N/m\); chiều dài tự nhiên \(l_1= 35cm\)­. Lò xo \(k_2\)_{­ ­}có độ cứng \(25N/m\), chiều dài tự nhiên \(l_2= 26cm\). Hai vật có khối lượng cùng bằng \(m\). Thời điểm ban đầu (t = 0), giữ lò xo \(k_1\) dãn một đoạn \(3cm\), lò xo \(k_2\) nén một đoạn \(6cm\) rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Bỏ qua mọi ma sát. Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động xấp xỉ bằng :

Cách giải :

- Tần số góc của vật 1 và vật 2 là : \(\left\{ \begin{array}{l}{\omega _1} = \sqrt {\dfrac{{{k_1}}}{m}}  = \sqrt {\dfrac{{100}}{m}}  = \dfrac{{10}}{{\sqrt m }}\\{\omega _2} = \sqrt {\dfrac{{{k_2}}}{m}}  = \sqrt {\dfrac{{25}}{m}}  = \dfrac{5}{{\sqrt m }}\end{array} \right. \Rightarrow {\omega _1} = 2{\omega _2}\)

- Lò xo k₁ có chiều dài tự nhiên l₁ = 35cm­. Lò xo k_{2 ­ ­}có chiều dài tự nhiên l₂ = 26cm

→ Vị trí cân bằng của hai lò xo cách nhau theo phương ngang 1 đoạn : \(35 – 26 = 9cm\)

- Thời điểm ban đầu (t = 0), giữ lò xo k₁ dãn một đoạn 3cm, lò xo k₂ nén một đoạn 6cm rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Chọn gốc toạ độ trùng với VTCB của lò xo k₁.

→ Phương trình dao động điều hoà của hai vật : \(\left\{ \begin{array}{l}{x_1} = 3\cos \left( {{\omega _1}t} \right) = 3\cos \left( {2.{\omega _2}t} \right)\\{x_2} =  - 9 + 6\cos \left( {{\omega _2}t + \pi } \right) =  - 9 - 6\cos \left( {{\omega _2}t} \right)\end{array} \right.\)

→ Khoảng cách giữa hai vật theo phương ngang trong quá trình dao động là : \(\Delta x = \left| {{x_1} - {x_2}} \right| = \left| {3\cos \left( {2.{\omega _2}t} \right) + 9 + 6\cos \left( {{\omega _2}t} \right)} \right|\)

Vì :

\(\begin{array}{l}\cos \left( {2.{\omega _2}t} \right) = 2{\cos ^2}\left( {{\omega _2}t} \right) - 1 \Rightarrow \Delta x = \left| {3\left( {2{{\cos }^2}\left( {{\omega _2}t} \right) - 1} \right) + 9 + 6\cos \left( {{\omega _2}t} \right)} \right|\\ \Rightarrow \Delta x = \left| {6.{{\cos }^2}\left( {{\omega _2}t} \right) + 6\cos \left( {{\omega _2}t} \right) + 6} \right|\end{array}\)

Đặt : \(a = \cos \left( {{\omega _2}t} \right) \Rightarrow \Delta x = \left| {6.{a^2} + 6a + 6} \right|\)

Ta có :

\(\begin{array}{l}6.{a^2} + 6a + 6 = 6\left( {{a^2} + a + 1} \right) = 6\left( {{{\left( {a + \dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}} \right) = 6.{\left( {a + \dfrac{1}{2}} \right)^2} + 4,5\\6.{\left( {a + \dfrac{1}{2}} \right)^2} + 4,5 \le 4,5 \Rightarrow {\left( {6.{a^2} + 6a + 6} \right)_{\min }} = 4,5\\ \Rightarrow \Delta {x_{\min }} = 4,5cm\end{array}\)

→ Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động là : \({d_{\min }} = \sqrt {M{N^2} + \Delta x_{\min }^2}  = \sqrt {{9^2} + 4,{5^2}}  = 10,06cm\)