Câu hỏi:
2 năm trước
Cho góc $AOB$ có số đo bằng $90^o$. Trong góc $AOB$ vẽ tia $OC.$ Trên nửa mặt phẳng bờ $OB$ không chứa tia $OC,$ vẽ tia $OD$ sao cho \(\widehat {AOC} = \widehat {B{\rm{OD}}}\). Tính số đo góc $COD.$
Trả lời bởi giáo viên
Đáp án đúng: d
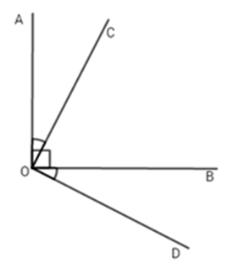
Vì $OC$ nằm giữa tia $OA$ và $OB$ nên:
$\widehat {AOC} + \widehat {COB} = \widehat {AOB}$ mà \(\widehat {AOB} = {90^0}\) (đề bài) \( \Rightarrow \widehat {AOC} + \widehat {COB} = {90^0}\) (*)
Mà \(\widehat {AOC} = \widehat {BOD} \) (đề bài)
nên từ (*) \(\Rightarrow \widehat {BOD} + \widehat {COB} = {90^0}.\, (1)\)
Lại có tia $OB$ nằm giữa tia $OC$ và $OD$ nên ${\rm{ }}\widehat {BOD} + \widehat {COB} = \widehat {COD}.\, (2)$
Từ (1) và (2) suy ra \(\widehat {COD} = {90^0}.\)
Vậy \(\widehat {COD} = {90^0}.\)
Hướng dẫn giải:
Sử dụng tính chất góc vuông, tính chất cộng góc để tính số đo góc $COD.$
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
