Câu hỏi:
2 năm trước
Cho đường thẳng $AB$ và điểm $O$ trên đường thẳng đó. Trên cùng một nửa mặt phẳng bờ $AB$ vẽ hai tia $OC$ và $OD$ sao cho \(\widehat {AOC} = \widehat {BOD} = {50^o}\). Trên nửa mặt phẳng bờ $AB$ không chứa tia $OD,$ vẽ tia $OE$ sao cho tia $OA$ là tia phân giác của góc $COE.$ Chọn câu đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
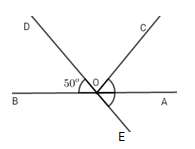
+ Hai góc $AOC$ và $BOD$ có: $OA$ và $OB$ là hai tia đối nhau, $OD$ và $OC$ không phải là hai tia đối nhau.
Vậy hai góc đó không phải là hai góc đối đỉnh.
+ Vì góc $BOD$ và $DOA$ là hai góc kề bù nên:
$\begin{array}{l}\,\,\,\,\,\widehat {BOD} + \widehat {DOA} = {180^O}\\ \Rightarrow {50^O} + \widehat {DOA} = {180^O}\\ \Rightarrow \widehat {DOA} = {180^O} - {50^O} = {130^O}\end{array}$
Tia $OA$ là tia phân giác góc $COE$ nên \(\widehat {AOE} = \widehat {AOC} = {50^O}\).
Tia $OD$ và tia $OE$ thuộc hai nửa mặt phẳng đối nhau bờ chứa tia $OA$ nên tia $OA$ nằm giữa hai tia $OD$ và $OE,$ ta có:
\(\widehat {DOA} + \widehat {AOE} = {130^0} + {50^0} = {180^0}\)
Suy ra $OD$ và $OE$ là hai tia đối nhau.
Hai góc $BOD$ và $AOE$ có hai cặp cạnh $OB$ và $OA,OD$ và $OE$ là hai tia đối nhau nên là hai góc đối đỉnh.
Hướng dẫn giải:
+ Xác định các tia đối, áp dụng định nghĩa hai góc đối đỉnh.
+ Áp dụng tính chất tia phân giác của một góc, tính góc $AOE.$ Áp dụng tính chất tia phân giác của một góc, tính tổng hai góc, chứng minh góc kề bù, từ đó xác định tia đối, hai góc đối đỉnh.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 5: đường thẳng vuông góc, đường thẳng song song - đề số 1 Toán 7 có lời giải chi tiết
