Câu hỏi tr 32
| Mở đầu: Bạn C đứng yên trên sân ga vẫy tay tiễn bạn A và bạn B trên tàu hỏa. Khi tàu chuyển động, bạn C thấy bạn B đang chuyển động ra xa trong khi bạn A lại thấy bạn B đứng yên trên tàu (Hình 5.1). Tại sao?
|
Phương pháp giải:
Liên hệ thực tế
Lời giải chi tiết:
Bạn C thấy bạn B đang chuyển động trong khi đó bạn A lại thấy bạn B đứng yên, sở dĩ như vậy là do tính tương đối của chuyển động, tùy vào vật đượcc họn làm mốc.
| 1. Quan sát Hình 5.2, mô tả chuyển động của: a) Bé trai (hình 5.2a) đối với mẹ trên thang cuộn và đối với bố cùng em gái đứng yên trên mặt đất. b) Thuyền giấy (hình 5.2b) đối với nước và đối với người quan sát đứng yên trên mặt đất.
|
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
a) Bé trai đứng yên so với mẹ và chuyển động xa dần so với bố cùng em gái.
b) Thuyền giấy đứng yên đối với nước và chuyển động xa dần đối với người quan sát.
Câu hỏi tr 33
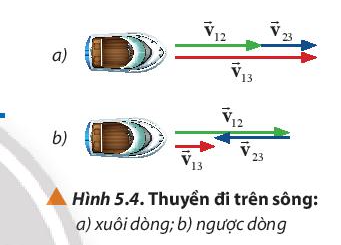
| 2. Em hãy đưa ra dự đoán để so sánh thời gian chuyển động của thuyền khi chạy xuôi dòng và khi chạy ngược dòng giữa hai vị trí cố định trên bờ sông (Hình 5.4)
|
Phương pháp giải:
Dự đoán
Lời giải chi tiết:
Từ hình vẽ, ta thấy thời gian chuyển động của hình a khi chuyển động xuôi dòng nhanh hơn thời gian chuyển động của hình b khi chuyển động ngược dòng.
Câu hỏi tr 34
| Luyện tập: Trên đường đi học, một bạn phát hiện để quên tài liệu học tập ở nhà. Vì vậy, bạn đó đã gọi điện thoại nhờ anh trai của mình đem đến giúp. Giả sử hai xe cùng chuyển động thẳng đều. Áp dụng công thức vận tốc tổng hợp, hãy giải thích trong trường hợp nào dưới đây bạn đó sẽ nhận được tài liệu nhanh hơn. a) Anh trai chạy đuổi theo bạn đó với vận tốc \(\overrightarrow {{v_{13}}} \) trong khi bạn đó tiếp tục chạy cùng chiều với vận tốc \(\overrightarrow {{v_{23}}} \) (v13 > v23 ). b) Anh trai chạy đến chỗ bạn đó với vận tốc \(\overrightarrow {{v_{13}}} \) trong khi bạn đó chạy ngược lại với vận tốc \(\overrightarrow {{v_{23}}} \) |
Phương pháp giải:
Biểu thức vận tốc tổng hợp: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Lời giải chi tiết:
Chọn chiều dương là chiều anh trai chạy đuổi theo.
Trong trường hợp a, ta có v13 > 0; v23 > 0
=> \({v_{12}} = {v_{13}} - {v_{23}}\)
Trong trường hợp b, ta có v13 > 0; v23 < 0
=> \({v_{12}} = {v_{13}} + {v_{23}}\)
=> Trong trường hợp b thì bạn đó sẽ nhận được tài liệu nhanh hơn.
Câu hỏi tr 35
| Luyện tập: Một đoàn tàu đang chuyển động đều với tốc độ 8 m/s và có một người soát vé đang ổn định khách trong toa tàu. Một học sinh đứng bên đường thấy người soát vé đi với vận tốc bằng bao nhiêu trong các trường hợp sau: a) Người soát vé đi với tốc độ 1,5 m/s về phía đuôi tàu. b) Người soát vé đi với tốc độ 1,5 m/s về phía đầu tàu. c) Người soát vé đứng yên trên tàu. |
Phương pháp giải:
(1) là vật chuyển động đang xét.
(2) là vật chuyển động được chọn gốc của hệ quy chiếu chuyển động.
(3) là vật đứng yên được chọn làm gốc của hệ quy chiếu đứng yên.
Biểu thức vận tốc tổng hợp là: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Lời giải chi tiết:
(1): người soát vé
(2): đoàn tàu
(3): học sinh.
Chọn chiều dương là chiều chuyển động của đoàn tàu. Ta có: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
a) Ta có v12 = 1,5 m/s; v23 = 8 m/s
Người soát vé đi về phía đuôi tàu, người soát vé chuyển động ngược chiều với chiều chuyển động của đoàn tàu nên ta có: \({v_{13}} = - {v_{12}} + {v_{23}} = - 1,5 + 8 = 6,5(m/s)\)
b) Ta có: v12 = 1,5 m/s; v23 = 8 m/s
Người soát vé đi về phía đầu tàu, người soát vé chuyển động cùng chiều với chiều chuyển động của đoàn tàu nên ta có: \({v_{13}} = {v_{12}} + {v_{23}} = 1,5 + 8 = 9,5(m/s)\)
c) Ta có: v12 = 0 m/s; v23 = 8 m/s
=> Vận tốc của người soát vé đối với học sinh là 8 m/s.
| Vận dụng: Nêu một số tình huống thực tế thể hiện ứng dụng tính chất tương đối của chuyển động. |
Phương pháp giải:
Liên hệ thực tế
Lời giải chi tiết:
Dòng nước đang chảy xuôi theo hướng từ Tây sang Đông, chiếc thuyền nếu đi theo hướng Tây sang Đông sẽ nhanh hơn chiếc thuyền đi ngược lại từ Đông sang Tây.
Bài tập
| 1. Một chiếc máy bay đang bay từ Thành phố Hồ Chí Minh đến Thủ đô Hà Nội với tốc độ 525 km/h. Trong hôm đó, gió thổi về hướng Nam với tốc độ 36 km/h. Xem như máy bay chuyển động thẳng đều theo hướng Bắc và quãng đường bay từ Thành phố Hồ Chí Minh đến Thủ đô Hà Nội là 1160 km. Hãy xác định thời gian bay của máy bay trên quãng đường đó. |
Phương pháp giải:
(1) là vật chuyển động đang xét.
(2) là vật chuyển động được chọn gốc của hệ quy chiếu chuyển động.
(3) là vật đứng yên được chọn làm gốc của hệ quy chiếu đứng yên.
Biểu thức vận tốc tổng hợp là: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Biểu thức tính thời gian của chuyển động thẳng đều: \(t = \frac{S}{v}\)
Lời giải chi tiết:
(1) máy bay
(2) gió
(3) mặt đất
Ta có vận tốc của máy bay so với gió là v12 = 525 km/h; vận tốc của gió so với mặt đất là v23 = 36 km/h
Chọn chiều dương là chiều chuyển động của máy bay (hướng bắc)
Do gió chuyển động theo hướng nam nên: \(\overrightarrow {{v_{23}}} < 0\)
Vận tốc của máy bay là:
\(\begin{array}{l}\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \\ \Rightarrow {v_{13}} = {v_{12}} - {v_{23}} = 525 - 36 = 489(km/h)\end{array}\)
=> Thời gian bay của máy bay trên quãng đường 1160 km là:
\(t = \frac{S}{v} = \frac{{1160}}{{489}} \approx 2,37(h)\)
| 2. Trong trận lũ lụt tại miền Trung vào tháng 10/2020, dòng lũ có tốc độ lên đến khoảng 4 m/s. Bộ Quốc phòng đã trang bị ca nô công suất lớn trong công tác cứu hộ. Trong một lần cứu hộ, đội cứu hộ đã sử dụng ca nô chạy với tốc độ 8 m/s so với dòng nước để cứu những người gặp nạn đang mắc kẹt trên một mái nhà cách trạm cứu hộ khoảng 2 km. a) Sau bao lâu đội cứu hộ đến được chỗ người bị nạn? Biết đội cứu hộ phải đi xuôi dòng lũ. b) Sau khi cứu người, đội cứu hộ phải mất bao lâu để quay lại trạm ban đầu? |
Phương pháp giải:
(1) là vật chuyển động đang xét.
(2) là vật chuyển động được chọn gốc của hệ quy chiếu chuyển động.
(3) là vật đứng yên được chọn làm gốc của hệ quy chiếu đứng yên.
Biểu thức vận tốc tổng hợp là: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Biểu thức tính thời gian của chuyển động thẳng đều: \(t = \frac{S}{v}\)
Lời giải chi tiết:
a)
(1) ca nô
(2) dòng nước
(3) bờ
Chọn chiều dương là chiều chuyển động của ca nô
Ta có v12 = 8 m/s; v23 = 4 m/s
Vận tốc của ca nô so với bờ là: v13 = v12 + v23 = 8 + 4 = 12 (m/s)
Đổi 2 km = 2000 m
Thời gian đội cứu hộ đến được chỗ người bị nạn là:
\(t = \frac{S}{v} = \frac{{2000}}{{12}} \approx 167(s)\)
b) Chọn chiều dương là chiều chuyển động của ca nô
=> Ca nô chuyển động ngược chiều dòng nước
=> v13 = v12 - v23 = 8 - 4 = 4 (m/s)
=> Thời gian đội cứu hộ quay về trạm ban đầu là:
\(t = \frac{S}{v} = \frac{{2000}}{4} = 500(s)\)